Calculus is the study of motion and rates of change. In fact, Isaac Newton develop Calculus (yes, like all of it) just to help him work out the precise effects of gravity on the motion of the planets! In this short review article, we’ll talk about the concept of average rate of change.
We’ll also talk about how average rates lead to instantaneous rates and derivatives. And we’ll see a few example problems along the way. So buckle up!

What is the Average Rate of Change of a Function
It all boils down to a simple formula from elementary physics. Suppose an object moves with a constant rate (or speed, or velocity). Then we can find the distance it covers over any specified time period using:
Distance = Rate × Time
However, it’s better to think about changes in distance and time. For example, if I drive from mile marker 25 to mile marker 35, that’s a distance of 10 miles (which is the change from 25 to 35).
(Change in Distance) = Rate × (Change in Time)
The rate can be found by dividing both sides by the Change in Time.
Rate = (Change in Distance) / (Change in Time)
Varying Rates
On the other hand, if the object’s rate does not remain constant, then the formula breaks down.
Think of a 10 mile car trip. If I tell you it took exactly 20 minutes to make the trip, then can you tell me my speed at any point in the journey?

Of course not!
You’d have no idea if I stopped at a red light 2 minutes into the trip, sped up to pass another car at the halfway point, or slammed on the brakes when the highway patrol showed up near the end of the trip.
On the other hand, if you did use the rate formula, you could still find out useful information.
Rate = (Change in Distance) / (Change in Time) = (10 miles) / (20 minutes)
= 0.5 miles/min.
Multiplying by the conversion factor, 60 min./hr., we find a speed of:
0.5 × 60 = 30 mph.
But what does this number represent? I may not have been traveling a constant 30 mph the entire trip, but if you smoothed out all of the slow and fast parts, then on average I was going 30 mph.
You’ve just computed my average rate of change, or average velocity.
Average Rate of Change Formula
Ok, next let’s talk about the precise formula.
In Calculus, most formulas have to do with functions. So let f(x) be a function. Let’s agree to treat the input x as time in the rate of change formula. The output, y = f(x), will be considered analogous to distance.
So, if rate = distance/time, then let’s define the (average) rate of a function to be the change in y-values divided by the change in x-values on a given interval. To simplify formulas, we often use the Greek capital delta ( Δ ) to stand for change.
The average rate of change of a function f on a given interval [a, b] is:
![]()
Notice how close this is to another important formula, the slope of a secant line.
![]()
In fact, they are the same formula! The average rate of change of a function on the interval [a, b] is exactly the slope of the secant line between the points at x = a and x = b.
Alternative Formula and the Derivative
Suppose now we specify that the point b is exactly h units to the right of a. In mathematics terms, b = a + h. How does this change our formula?
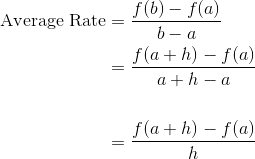
Does the last line look familiar?
If you replace a by x (to make it more like a function), and allow the difference h to approach 0 by taking a limit, then you get the definition of derivative of the function.
![]()
After we apply the limit, we often call this formula the instantaneous rate of change, or instantaneous velocity.
So the notion of rate of change serves as a launchpad into the study of limits and derivatives, the heart of differential Calculus!
Relation to the Mean Value Theorem
There is an important mathematical result called the Mean Value Theorem (MVT). Basically, the MVT states that any function that is continuous and differentiable on an interval must have a point inside that interval at which the instantaneous rate of change (derivative) must equal the average rate of change over the interval.
In mathematical notation, ![]() for some c such that a < c < b.
for some c such that a < c < b.
For a nice review of the MVT, you might want to check out: AP Calculus Review: Mean Value Theorem.
You can expect to see a question or two about the MVT, so it’s good to be aware if its connection with average rates of change.
Example Problems
Let’s take a look at a couple problems, shall we?
Problem 1
An object travels in a straight line according to the formula x = 3t2 – 2t + 1, for 0 ≤ t ≤ 8. Find the object’s average velocity on the given time interval.
Solution
Be careful! In this problem, the input variable is t while the output is x. Therefore, the average velocity formula takes the form Δx / Δt.
The given interval is [0, 8], so we use a = 0 and b = 8 in the formula.
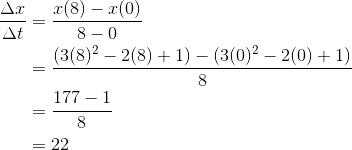
The average velocity is 22.
Problem 2
Find any point between 1 and 9 such that the instantaneous rate of change of f(x) = x2 at that point matches its average rate of change over the interval [1, 9].
Solution
This is a job for the MVT! Notice how we must set the derivative equal to the average rate of change.
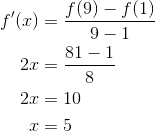





Leave a Reply