Mathematics is a language. You need to know the terms and notation in order to successfully master the concepts. Out of the hundreds of key words you might find in your textbook, I’ve complied a list of the top ten AP Calculus vocabulary words, which I hope will give you a good foundation for further study.
The words on this list (with one exception) pertain to both the AB and BC versions of the AP Calculus test.
And so, without further ado, here’s your top ten!
Top Ten AP Calculus Vocabulary Words
1. Limit
The limit of a function y = f(x) (as x approaches a number a) is something like the ultimate trend of the values of f (near x = a).
The limit notation, ![]() , stands for the phrase: “The values of f get closer and closer to y = L as the x-values approach a.”
, stands for the phrase: “The values of f get closer and closer to y = L as the x-values approach a.”
It’s essential to understand both what a limit is conceptually as well as how to find limits graphically, analytically, and by algebraic manipulation.
For more about limits, check out: What is the Limit of a Function?
2. Continuous
We say that a function f is continuous at a x = a if the value of f(a) matches the predicted value coming from the limit as x → a. That is,
In more intuitive terms, this means that there is no break or hole in the graph at x = a.
We also say that a function is continuous on an interval if it’s continuous at each individual point in that interval. Some teachers say that a function is continuous on an interval if “you can draw the graph without lifting your pencil” on that interval.
Take a look at the following brief review for more information: AP Calculus Exam Review: Limits and Continuity.
3. Derivative
The derivative of a function f is a (typically different) function f ' that measures the rate of change of the y-values of f with respect to change in the x-value. Another notation for the derivative is dy/dx.
The derivative value f '(a) also measures the slope of the tangent line to the curve at the point (a, f(a)).
There are a number of formulas that go along with this definition. First and foremost, the limit definition of the derivative is based finding the slope of the tangent line using a limit. It’s valid for all functions but is hard to work with, especially for complicated functions.
![]()
Other formulas, such as the Power Rule, Product and Quotient Rules, and Chain Rule, serve to find derivatives of all kinds of functions.
For more about derivatives and the various derivative formulas, check out Calculus Review: Derivative Rules.
4. Velocity (and Acceleration)
Suppose an object moves along a straight line over time, and suppose the function s(t) measures the position of the object at any time t. Then the velocity of the object, as a function of time, is the derivative of position. That is, v(t) = s '(t).
The reason for this is that velocity is the rate of change of position (see item 3 above).
The rate of change of velocity is called acceleration. And so acceleration is the derivative of velocity. In other words, acceleration is the second derivative of position.
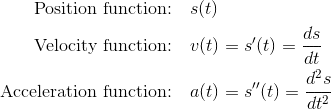
5. Chain Rule
Among all of the derivative rules you have encountered, perhaps the most useful and yet most misunderstood is the chain rule. The chain rule is a formula for finding the derivative of a composition of functions.
![]()
What makes this rule so important is that so many important functions are actually compositions of two or more basic functions.
You can find more details about the chain rule, along with worked out examples, by clicking AP Calculus Review: Chain Rule.
6. Logarithm
The logarithm of a number is equal to the exponent on a given base that would give that number. For example, the logarithm in base 2 of the number 32 is 5. Why? Because 32 = 25.
But that’s algebra not calculus, right? How did logarithm make it to the Top Ten AP Calculus Vocabulary Words?

Well there are two big reasons.
First, there is a particular number called e that goes into defining the natural logarithm. The number e is roughly 2.7, but it’s not crucial to memorize the constant itself.
Instead, you’ll need to be aware of the properties of the natural logarithm and its close cousin, the natural exponential function, ex.
Second, logarithms play a huge role in certain derivative formulas. The technique of logarithmic differentiation uses the natural logarithm, ln x, to break down powers, products, and/or quotients into simpler operations so that it’s easier to apply your derivative formulas.
Be sure to brush up on your logarithms before the test. Here’s an article to help you do just that: AP Calculus Review: Properties of Exponents and Logarithms.
7. Slope Field
A slope field is a certain kind of visualization of a differential equation.
Suppose you have a differential equation of the form dy/dx = …, where the dots represent an expression involving both x and y. The slope field is found by plugging in sample points (x, y) and drawing short segments of slope equal to the value of dy/dx that you get at each point.
For example, below is the slope field of dy/dx = x + y.
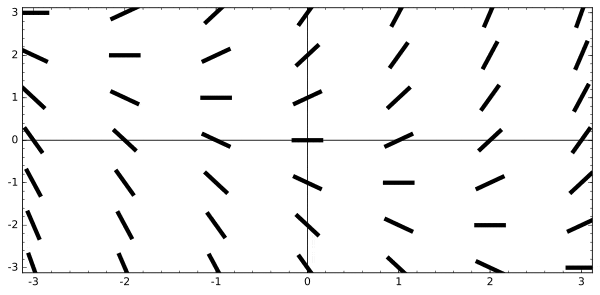
While it may seem at first that slope fields are hard to grasp, they are actually quite intuitive. I like to think of the slope field as a map of the currents in a river. Then any particular function that solves the differential equation is really just a path of a boat through the water along those currents.
8. Integral
Integrals form a huge part of the AP Calculus exam. In fact you might say they are an… (wait for it)…. integral part of the test!
Integration is the reverse operation of differentiation, but of course there’s much more to the story.
For a good review of integrals, check out: AP Calculus Exam Review: Integrals
9. Series (BC only)
A series is the sum of a sequence of numbers.
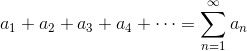
When studying series you have to be aware of terms like convergent, divergent, integral test, conditionally convergent, alternating, etc.
Moreover, once you have series of numbers mastered, then they throw series of functions at you! Those are called Taylor series or Maclaurin series.
If you want a detailed review of this topic, take a look at this review of sequences and series.
10. Theorem
Last but not least, let’s talk about theorems in mathematics. A theorem is simply a true mathematical statement.
For the AP Calculus exams, you’ll need to understand and be able to apply various theorems, including:
- Extreme Value Theorem (EVT)
- Mean Value Theorem (MVT)
- Rolle’s Theorem
- The Fundamental Theorem of Calculus (FTC)
Check out AP Calculus Review: Reasoning with Theorems and Definitions for more.
Summary
Here’s that list of AP Calculus vocabulary one more time. Happy studying!
- Limit
- Continuous
- Derivative
- Velocity (and Acceleration)
- Chain Rule
- Logarithm
- Slope Field
- Integral
- Series
- Theorem





Leave a Reply