Often when we are trying to find the roots of a function, the algebraic methods we learned in earlier math classes are either tedious or impossible. Newton’s Method allows us to overcome this. Imagine trying to find the roots of f(x) = x4 – 3x2 + 2x – 1. We know that the equation has either 0, 2, or 4 real roots, although just looking at it, this would not be obvious.
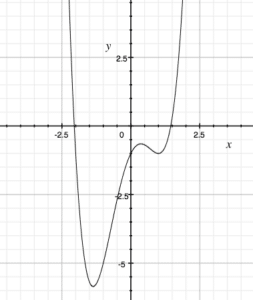
The graph shows us that the equation indeed has 2 roots, but we are still not sure what these roots are (although our graphing calculator can solve this for us; see our post on Calculator Strategies for the AP Calculus Exam for more).
Newton’s Method is an iterative method to find approximate roots of equations.
Newton’s Method usually does not give the exact answer, but will allow us to find very exact approximations. The fist requirement for Newton’s Method is that we know the derivative of the function.
Let’s walk through an example to show where Newton’s Method comes from.
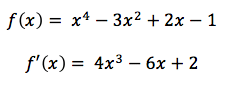
First step: Take a random guess as to what the root might be. Let us choose x = 2 for this first guess. We’ll call this x0. Depending on our initial guess, our method might find the first or the second root.
Second step: Find the equation of a line tangent to the curve at the point x0.
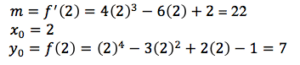
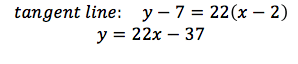
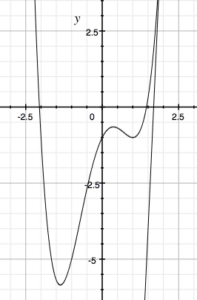
Notice our tangent line has its own root close to the root of our original equation. It is easy to find the root of a linear function. If we take the root of y = 22x-37, we get 37/22, which is about 1.682. This isn’t a perfect approximation, but it’s close. If we were to repeat this entire method, using x = 1.682 instead of x =2, we would get an even closer approximation.
Now there is a quick formula that you can derive that gives us our sequence of increasingly accurate approximations.
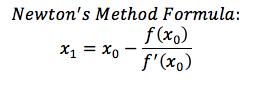
Plugging in x0 = 2, we get x1 = 1.682, exactly what we found above. If we do this a few times, we see that we get increasingly close to our root:
x0 = 1.682
x1 = 1.51
x2 = 1.454
x3 = 1.448
Each step brings us closer and closer to the root. We’ll never get perfectly there in this example, but within 4 steps, we’ve within .001. A few more steps, and we’d be within millionths of the correct answer.
Newton’s Method is an extremely efficient way of finding approximate roots to equations. It works even if the equation is incredibly complicated or would be impossible or difficult to algebraically find exact roots. It rarely gets an exact correct answer, but allows us to get very close. Numerical methods, such as Newton’s Method, for finding roots are the way many computer programs (including many graphing calculators) find answers to equations. The requirement for Newton’s Method is that you know the derivative of the function.
Now let’s practice:
Take f(x) = x2 – 9. You know the answer to this equation is +/- 3. Try Newton’s Method with this equation to see how many iterations it takes to get within a few thousands of the correct answer.





Leave a Reply