Of all the derivative rules it seems that the Chain Rule gets the worst press. Many students dread the rule, think that it’s too difficult, don’t fully understand where to apply it, and generally wish that it would go away.
Are you in this group?
If so then I hope that by the end of this short article, you’ll gain a better appreciation for the Chain Rule and how it is used in derivative problems.
The Chain Rule
We use the Chain Rule to find the derivative of a composition of functions, that is a function of the form f(g(x)).
What is a Composition?
if f(x) and g(x) are two functions, then we call f(g(x)) the composition of f and g. We might call f the “outside” function, and g the “inside” function.
For example, if f(x) = sin(x), and g(x) = x2 + 1, then their composition is:
f(g(x)) = sin(x2 + 1).
Decomposition
To use the Chain Rule properly, you need to know how to go the other direction. In other words, you have to learn how to decompose a composite function into a pair of functions — the outside and inside functions.
To make it clearer, we often use a different variable name, such as u, for the input variable of the outside function.
For example, if y = (4x – 2)3, then the most natural decomposition would be:
(Outside function, or f(u)): y = u3, and
(Inside function, or g(x)): u = 4x – 2.
Statement of the Chain Rule
Suppose f and g are differentiable functions. Then the composite function, f(g(x)) is also differentiable, and
![]()
I think of this as a 3-step process.
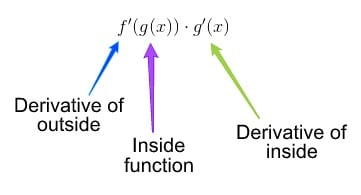
- Find the derivative of the outside.
- Plug in the inside function.
- Multiply by the derivative of the inside.
Equivalently, if y = f(u), and u = g(x), then
![]()
Here, the rule has been written in Leibniz notation, and clearly expresses the fact that the derivative of a composition is really just the product of the derivatives of the individual functions. Just don’t forget that step of plugging back in u = g(x).
Example
Find the derivative of ![]() .
.
First decompose the function.
(Outside function): f(u) = ![]() .
.
(Inside function): g(x) = x2 + 1.
Following the three-step process,
- First find the derivative of the outside:

- Next, plug in the inside function:

- Finally, multiply by the derivative of the inside:

Now that we have found the derivative correctly, let’s simplify the final answer using algebra.
![]()
Conclusion
Use the Chain Rule to find the derivative of a composition. Always keep in mind the 3-step process:
- Find the derivative of the outside.
- Plug in the inside function.
- Multiply by the derivative of the inside.





Leave a Reply