What is the logistics growth model, and how does it work in problems on the AP Calculus BC exam? This review article will explain what you need to know for the test.

The Logistics Growth Model
The logistics growth model is a certain differential equation that describes how a quantity might grow quickly at first and then level off.
Let y stand for the quantity, which is often population. In the logistics model, the rate of change of y is proportional to both the amount present and the different between the amount and a fixed carrying capacity, M.
In mathematical language, we would say there is a positive constant k such that:
![]()
The following equivalent form of the equation is also useful (though the constant k may have a different value).
![]()
Interpreting the Model
Most often on the AP Calculus BC exam, your job will be to interpret the model. You should be able to find out characteristics of the model without explicitly solving for y.
Based on the form of the differential equation, we can find the general shape of the logistics model. The resulting graph is the logistics curve.
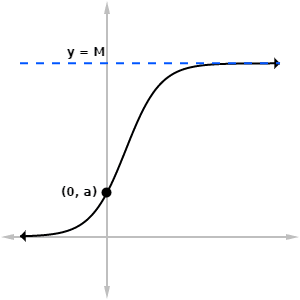
There are a few important things to note.
- The value of y always increases over time. (It’s a growth model, after all!)
- As t → ∞, the value of y tends to M. This means that in the long run, the population tends to approach its carrying capacity. It will never exceed M. In fact, y will never actually reach M, but just get arbitrarily closer.
- Related to the last point, the line y = M is a horizontal asymptote for the curve. (See How do you Find the Horizontal Asymptotes of a Function? for more details.)
- The curve passes through a certain initial value, y = a. We’ll talk more about this below.
Example 1
Find the limit of the function P(t) as t → ∞ if P ' = 7.2P(3200 – P).
Solution
First of all, you have to recognize it’s a logistics model problem. Otherwise, you might lose valuable time trying to solve the differential equation.
In this question, we can identify k = 7.2, M = 3200, and treat the variable P just like y in the logistics model.
We know that the value of P must approach the carrying capacity. According to the form of the equation, that would be M = 3200.
So just like that, with hardly any work at all, you got the final answer! It pays to know your concepts rather than have to work everything out from scratch.
The Logistics Function
Even though most problems about the logistics growth model involve the differential equation itself, you also need to know its general solution.
The solution to the logistics differential equation, ![]() is:
is:
![]()
Here,
- M is still the carrying capacity.
- k is a positive constant that controls rate of growth.
- b is a constant that helps to control where the curve crosses the y axis.
In fact, a = M/(1+b) is the y-intercept, or initial value.
Example 2
Find the carrying capacity and initial population if the population fits the following model.
![]()
Solution
As before, just recognizing that this is a logistics growth model is key.
This time, though, we have the “solution” function rather than the differential equation. But just compare this to the known solution, identifying M = 108,000 and b = 17.
The carrying capacity is M = 108,000.
The initial population is a = M/(1+b) = 108,000/(1 + 17) = 6000.





Leave a Reply