Taylor and Maclaurin series are like polynomials, except that there are infinitely many terms. What makes these important is that they can often be used in place of other, more complicated functions. Read on to find out how!
Taylor and Maclaurin Polynomials
First of all, let’s recall Taylor Polynomials for a function f. You might want to read up on the topic here: AP Calculus BC Review: Taylor Polynomials
Assume n ≥ 0 is a fixed whole number. (This is the degree, or order, of the polynomial.)
Moreover, let’s assume c is a fixed real number (called the center).
Then the Taylor polynomial of f is:
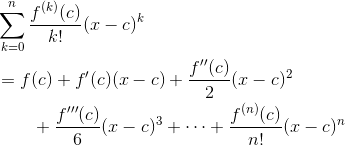
And the Maclaurin polynomial is just the Taylor polynomial centered at c = 0.
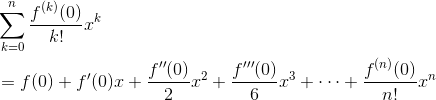
Approximating Functions
Taylor and Maclaurin polynomials can approximate a function to any desired level of accuracy.
For example, see the figure below for graphs of the first few Maclaurin polynomials for f(x) = sin x.
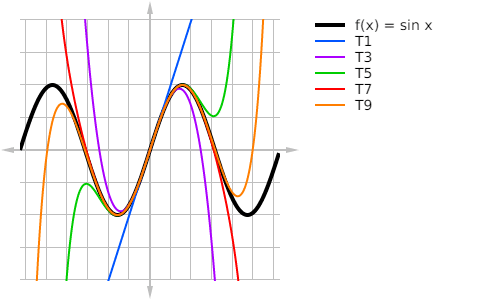
Taylor and Maclaurin Series
But Taylor and Maclaurin polynomials can only approximate functions. The approximation gets better and better with the inclusion of more terms. If you want an exact answer, then you have to include all the terms — all of the infinitely many terms!

So a Taylor series is really just taking a Taylor polynomial to its logical extreme — what happens when we let a Taylor polynomial’s degree increase without ever stopping?
Note, we still use the same formula for the Taylor coefficients as we did for Taylor polynomials:
![]()
(Remember, the superscript (n) means the nth derivative, not the nth power, of the function.)
Here’s the complete formula for the Taylor series of f, with center c (Taylor’s Formula):
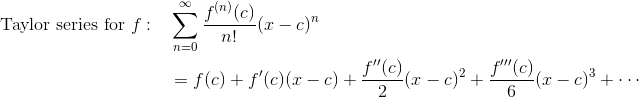
The Maclaurin series is the same thing, but with c = 0 plugged in.
Convergence Issues
Because there are an infinite number of terms in a typical Taylor series, we have to address questions of convergence.
The convergence of a Taylor or Maclaurin series depends on the value of x. A given series will do one of three things:
- It may converge (have a finite value) regardless of x.
- There may be a finite number R (called the radius of convergence) so that the series converges within R units of the center c, and diverges outside of those bounds.
- The series may converge only at the center x = c, diverging at every other x-value.
But wait, it gets worse!
Sometimes, even if a Taylor series for f converges at some x-value, it may not actually have the same value as f(x)!
Don’t worry, though. On the AP Calculus BC exam, you will only see situations in which the Taylor series converges to the function within some finite radius or for all x.
In this article, we’ll just focus on producing Taylor and Maclaurin series, leaving their convergence properties to another post.
Differentiation and Integration
Taylor series are a type of power series. As such, you can do term-by-term differentiation and integration.
The following derivative and integral formulas apply to any power series — not just Taylor series.
Derivative Formula
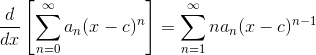
Integral Formula
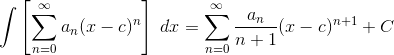
Common Power Series
Some functions are so common and useful that it just makes sense to memorize their power series.
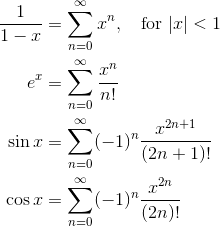
There is no Maclaurin series for ln(x), because ln(0) is undefined. However, there’s a quick and easy fix. Just shift the function itself over by one unit.
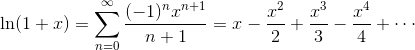
Example: Hyperbolic Functions
The two functions, hyperbolic sine (sinh x) and hyperbolic cosine (cosh x) show up often in engineering.
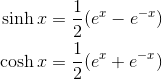
Find the Maclaurin series for each one. Then I’ll show you two methods. You can pick which one seems better for you.
Solution #1
First, let’s see if we can use Taylor’s Formula.
We’ll need to know the derivatives of both sinh x and cosh x. Fortunately, there is a very simple pattern.
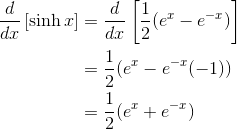
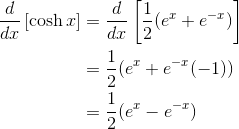
Notice anything?
The derivative of sinh x is just cosh x, and vice versa!
Next, we’ll also need to know the values at c = 0.
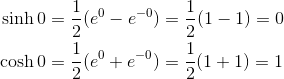
Now we have everything we need to put together the power series.
| k | f(k)(x) | f(k)(1)/k! |
|---|---|---|
| 0 | f(x) = sinh x | sinh 0 = 0 |
| 1 | f '(x) = cosh x | cosh 0 = 1 |
| 2 | f ''(x) = sinh x | (sinh 0)/2! = 0 |
| 3 | f '''(x) = cosh x | (cosh 0)/3! = 1/6 |
| 4 | f(4)(x) = sinh x | (sinh 0)/4! = 0 |
| 5 | f(5)(x) = cosh x | (cosh 0)/5! = 1/120 |
Only the odd degree terms are nonzero. Here’s what it looks like when you put it all together.
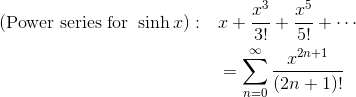
The power series for cosh x follows much the same pattern, except that now it’s the even degree terms that are nonzero.
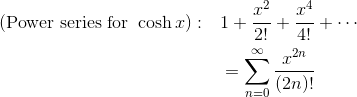
Solution #2
Now let’s use the known power (Maclaurin) series for ex to derive a power series for sinh x and cosh x.
Remember: 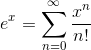 .
.
Then, in the formula for sinh x, you can just use the series for ex everywhere you see an “ex.”
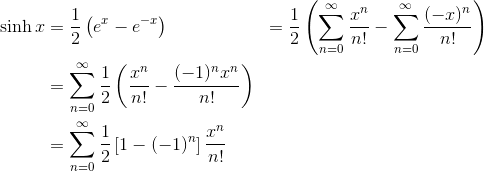
That last line may be simplified further. There is a pattern at work here.
- If n is even, then 1 – (-1)n – 1 – 1 = 0.
- But if n is odd, then 1 – (-1)n – 1 – (-1) = 2.
So actually, only the odd degree terms survive in the sum. (Sound familiar?)
And in that case, the 1/2 cancels with the 2, so that only the power of x and the factorial remains in each term.
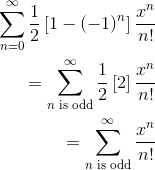
Finally, by re-indexing the sum in terms of odd whole numbers (2n + 1), we get the proper Maclaurin series for sinh x.
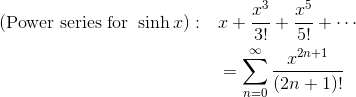
You can do the same sort of work to derive the series for cosh x. The first few steps are shown below, but the result will be the same series that we got before for hyperbolic cosine.
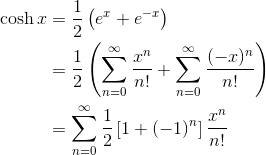
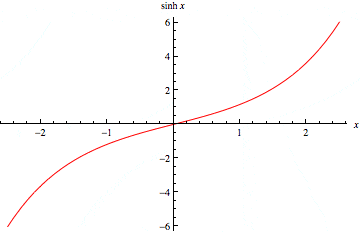
Graphs of Hyperbolic Functions
Finally, to round out this example problem, let’s take a look at the graphs of each hyperbolic function. It would be a great exercise for you to plot the first few Taylor polynomials of each series and compare the results against these graphs.





Leave a Reply