Whenever you work with a power series, you have to be careful about its radius and interval of convergence. This article reviews the definitions and techniques for finding radius and interval of convergence of power series. And we’ll also see a few examples similar to those you might find on the AP Calculus BC exam.
The Radius and Interval of Convergence
Recall that a power series, with center c, is a series of functions of the following form.
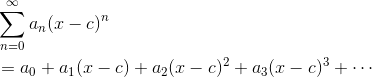
Now anytime you have an infinite series (infinitely many terms), you have to worry about issues of convergence. In fact, the series may converge (have a finite sum) for some values of x, but diverge at others.
For more about convergence and divergence in general, check out: AP Calculus BC Review: Series Convergence.
Three Possibilities
There are three things that could happen.
- The series converges regardless of x.
- There may be a limited range of x-values, called the interval of convergence, for which the series converges. And the series diverges outside of that interval.
- The converges only at the center x = c, diverging at every other x-value.
Now, that second point is probably the trickiest. When a series has a finite interval of convergence, then it’s always centered at… well… the center!
In other words, there would be a finite positive number R, called the radius of convergence, such that the series converges for all x-values that are within R units from the center c. Any x-values greater than a distance of R from c would cause the series to diverge.
But what about those points that are exactly R units away? That is, c – R and c + R?
Here, there are a number of possibilities as well. The series could converge or diverge at each of the two endpoints. See the table below for the four combinations.
| Behavior at left endpoint, c – R |
Behavior at right endpoint, c + R |
Interval of convergence | Interval of convergence as an inequality |
|---|---|---|---|
| Converges | Converges | [c – R, c + R] | c – R ≤ x ≤ c + R |
| Converges | Diverges | [c – R, c + R) | c – R ≤ x < c + R |
| Diverges | Converges | (c – R, c + R] | c – R < x ≤ c + R |
| Diverges | Diverges | (c – R, c + R) | c – R < x < c + R |
Techniques for the Finding Interval of Convergence
There are typically two phases to finding the interval of convergence.
- First, find the radius of convergence, R. Usually the root or ratio test works best for this part.
- Second, find out the behavior of the series at each of the two endpoints, c – R and c + R. This time, do not use root or ratio tests, as those will almost certainly give you inconclusive results at the endpoints. Instead, you may use comparison, limit comparison, alternating series test, integral test, p-series test, or other appropriate tests.
Example 1
Determine the interval of convergence for the series.
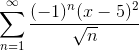
Solution
First, observe that the center of this series is 5. You find that by looking for the part of the general term that looks like (x – c), and looking to see what c must be there.
Let’s use the root test. When working with power series, we start by setting the limit less than 1 (for convergence). Then, after taking limits (as n → ∞), you’ll be able to solve for an expression of x, giving you the radius of convergence explicitly.
The algebra can get a little hairy…
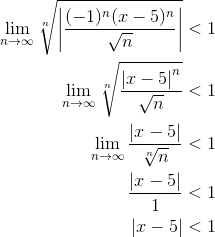
Thus, the radius of convergence is R = 1 (from the right side of the inequality).
Now with center at 5, and radius 1, we can figure out the two endpoints.
- c – R = 5 – 1 = 4.
- c + R = 5 + 1 = 6.
So already, we have four possibilities to work with. We know that the interval of convergence must be from 4 to 6, but we just don’t know yet whether or not to include any of the endpoints.
Now let’s plug in each endpoint for x, and work out the convergence properties.
- At x = 4:

The resulting series is a p-series with p = 1/2 (because of the square root of n in the denominator).
By the p-series test, this series diverges. Therefore, 4 is not in the interval of convergence.
- At x = 6:

This time, in addition to the square root in the denominator, there is also a factor of (-1)n. This makes a huge difference. Now we’re looking at an alternating series, which is much more likely to converge.
In fact, the series does converge, since the absolute value of the general term limits onto zero.

Thus by the Alternating Series Test, this series converges. So x = 6 must be included in the interval of convergence.
(For more details about alternating series and the Alternating Series Test, check out: AP Calculus BC Review: Alternating Series.)
Summarizing the above work, we know that 4 is not included, but 6 is. Therefore, the interval of convergence is: (4, 6], or 4 < x ≤ 6.
Example 2
What is the largest interval on which the Maclaurin series for the exponential function converges?
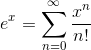
Solution
This time, the ratio test will be best. Again, we will set the limit less than 1. But first let’s figure out what the limit will be.
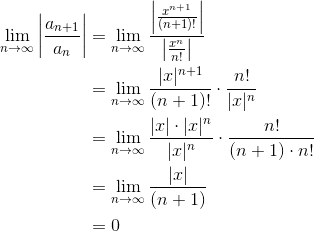
The reason that we get a limit of zero this time is because the numerator |x| must be considered fixed as n → ∞. Of course the denominator explicitly involves n. So in the limit, we get constant/∞, which is simply 0.
Now, regardless of what value x has, the left side of the inequality will always be 0. Setting 0 < 1 produces a trivial true statement, so no matter what x is, the sequence converges!
In this situation, we say that the radius of convergence is infinity (R = ∞), and the interval of convergence is the entire real number line, (-∞, ∞).
Summary
Given a power series centered at c,
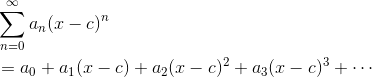
- The radius of convergence, R, is the largest number such that the series is guaranteed to converge within the interval between c – R and c + R.
- The interval of convergence is the largest interval on which the series converges.
- If R is finite and nonzero, then there are four combinations for interval of convergence, depending on whether each endpoint is convergent or not in the series.

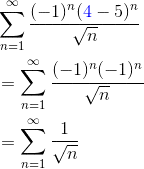
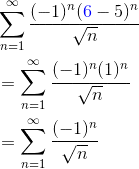
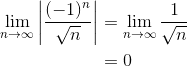




Leave a Reply