Substitution is just one of the many techniques available for finding indefinite integrals (that is, antiderivatives). Let’s review the method of integration by substitution and get some practice for the AP Calculus BC exam.
The Substitution Rule
Integration by substitution, also known as u-substitution, after the most common variable for substituting, allows you to reduce a complicated integral to one that is easier to work with.
The formula works as follows. Suppose that F is an antiderivative for f. Then we have:
![]()
In fact, you can think of the Substitution Rule as reversing the Chain Rule.
Basically, this rule states that if you have a complicated integral like the one on the left, then it instantly reduces to a simpler one that can be worked out with no trouble.

However, the hard part is arranging a given integral in the right way. That’s where the step-by-step method outlined below comes in.
Furthermore, substituting isn’t a magic bullet that can tackle every integral. Just think of it as one powerful tool in your toolbox. For more tools and information about integration, check out the following resource. AP Calculus Review: Indefinite Integrals.
The Method of Integration by Substitution
Next let’s review the main steps in u-substitution.
Step 1. Choose Your Substitution
If you want to use substitution, then the first thing to do is to identify what you want to substitute.
In other words, you have to make a choice for what u = g(x) will be in your integral.
But what should you choose? That comes with experience.
There are a few good rules of thumb to follow when choosing u, but these are by no means fool-proof. So if the first choice doesn’t work, try something else.
- Expression within a set of parentheses
- Expression within a radical
- Denominator (if the integrand is a single fractional expression)
- Either sin x or cos x if the other trig function is also present
- Exponent of e
- Trig (reverse) Substitution
Step 2. Find the Differential
Once you’ve decided on your substitution, the next step is to find its differential. Remember, the differential of a function of x is just its derivative times dx.
So the differential of u = g(x) is du = g ‘(x) dx,
The reason you should do this step is that the differential provides a link between the “dx” from the original integral and the new integral, which will have “du” instead.
Step 3. Rewrite the Integral
Now you get to change the form of the integral.
Replace g(x) by u, hopefully making the integrand a little simpler.
But don’t be worried if there are still expressions in the integral involving x. In fact, those leftover expressions can be traded out using du = g ‘(x) dx.
The only catch is that you have to have a perfect match in order to make the trade. We’ll see more about this point in the examples below.
Step 4. Simplify and Integrate
Next, check to see what variables are represented in the integral. If there are any leftover x‘s anywhere, or if the old differential dx is still in the integral, then the substitution is not complete.
However if there are only expressions of u, and if the differential is du, then you can move on to the integration step.
Simplify the integrand as much as possible. Hopefully the result is a much simpler integral (in the variable u) than the one you started with (in x).
Now is the time to integrate!

Step 5. Replace the Substitution
Assuming you made it this far, you now have a function of the variable u (plus a constant of integration). The final step is to replace every u by its expression in x, namely the function g(x) that you chose back in Step 1.
Examples
Ok let’s see if we can use the method of integration by substitution in a few examples.
Example 1 — An Exponential Experience
![]()
Solution
The best choice for substitution would be the exponent of e. That is, u = x2.
Then the differential would be: du = 2x dx.
However there is no constant 2 in the original integral. The best way I’ve found to deal with mismatched constants is to divide them from both sides of the differential: ![]() .
.
Then we can make our substitutions and solve the integral. Don’t forget to replace your substitution at the end!
I’ve used blue for the u-substitution and red for its differential to make the process a little clearer.
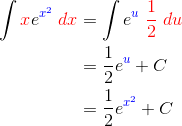
Example 2 — A Bit Trig-ier
![]()
Solution
This one is tricky. In fact, a simple integration by substitution won’t work. Not until we rewrite the integrand using a trig identity, that is.
Remember the Pythagorean Identity? Well it can be used to exchange squared powers of sine for cosine and vice versa.
![]()
The key step here is to isolate a single factor of cos x and convert the remaining factor into an expression of sin x using the Pythagorean Identity.
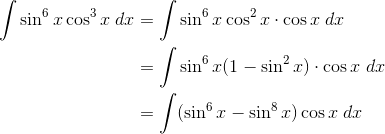
Now we can see what the substitution will be. Let u = sin x.
Then the corresponding differential is: du = cos x dx.
Fortunately, there is a perfect match for the differential this time. So the rest of the process is fairly straightforward. Just remember that sinn x stands for (sin x)n.
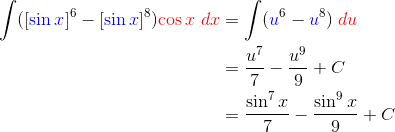
Example 3 — Trig Substitution (Challenging)
![]()
What’s Our Gameplan?
As far as substitution problems go, this one is by far the hardest type that you may find on the AP Calculus BC test.
The first natural choice for substitution, u = 4 + x2, won’t work. The reason is that the differential, du = 2x dx, has that extra “x” in it that cannot be matched in the integrand.
Instead, we will make something like a reverse substitution, called a trig substitution.
When you have an expression like a2 + x2, then the trig substitution x = a tan θ often helps.
Why? Because of the identity, 1 + tan2 θ = sec2 θ.
(Note, there are two other kinds of trig substitution. For more details, check out this video.)
Let’s see how a trig substitution can help us out in this situation.
Solution
Substitute x = 2 tan θ
The differential is: dx = 2 sec2 θ dθ, which tells us exactly how to replace dx in the original integral. Warning: this could get messy!
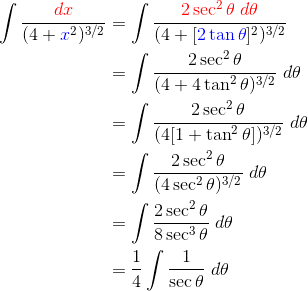
Now after all that work, we’re in the home stretch! Simply rewrite the reciprocal of secant in a more useful form and integrate.
![]()
Finally, we have to reinterpret the answer in the original variable x.
The best way to do this is to think trigonometrically. Based on our chosen substitution, x = 2 tan θ, we know that tan θ = x/2.
Interpret this information in a right triangle. The opposite side could be x while the adjacent side is 2. That makes the hypotenuse equal to: ![]() (Doesn’t that expression look familiar?)
(Doesn’t that expression look familiar?)
Therefore, sin θ, which is opposite over hypotenuse, is equal to:
![]()
Putting it all together,
![]()
Conclusion
Integration by substitution is a powerful tool that gets used quite often in practice. It’s worth your time to master this technique in order to score as high as possible on the AP Calculus BC exam.





Leave a Reply