What is a geometric series? A series is the sum of the terms of a sequence. What makes the series geometric is that each term is a power of a constant base. For example,
![]()
Each term in this series is a power of 1/2. Equivalently, each term is half of its predecessor. Whenever there is a constant ratio from one term to the next, the series is called geometric.
Read on to find out more!
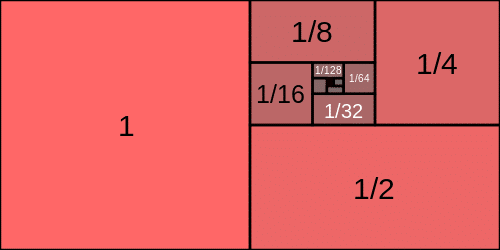
Infinity and Zeno’s Paradox
Typically there are infinitely many terms to add up in a series. So it’s usually very difficult to determine whether the answer is finite, let alone what the value of the sum could be.
But how can you add up infinitely many terms in the first place???
This question puzzled the ancient Greek philosophers and mathematicians. In fact, the idea of infinity perplexed Zeno of Elea (c. 490 – c. 430 BC) so much that he concluded that motion must be impossible.
Of course we all experience motion every day. In a real life race between Achilles and the Tortoise, we all know that Achilles would eventually overtake the slowpoke Tortoise.
The key is a geometric series. Even though there may be an infinite number of lengths that Achilles must get through to catch the Tortoise, each length itself is smaller by a constant ratio compared to the last. When you add up the terms — even an infinite number of them — you’ll end up with a finite answer!
Geometric Series
A geometric series is the sum of the powers of a constant base r, often including a constant coefficient a in front of each term.
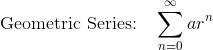
![]()
So, each of the following is geometric.
- 1 + 3 + 9 + 27 + 81 + … (r = 3, a = 1).
- 2/3 – 2/9 + 2/27 – 2/81 + … (r = -1/3, a = 2/3).
- 1 – 1 + 1 – 1 + 1 – 1 + … (r = -1, a = 1).
On the other hand, the following series are not geometric.
- 2 + 4 + 6 + 8 + 10 + … (arithmetic sequence with common difference d = 2)
- 1 + 4 + 9 + 16 + 25 + 36 + … (sum of squares)
- 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + … (Harmonic Series)
Convergence and Divergence
There is a straightforward test to decide whether any geometric series converges or diverges.
- If |r| < 1, then the series converges.
- If |r| ≥ 1, then the series diverges.
Furthermore, whenever the series does converge, there is a simple formula to find its sum:
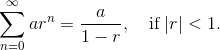
Proof of the Sum Formula
In order to really understand why the formula works the way it does, let’s dig into a proof of the result.
First of all, let’s see what the kth partial sum of the series Σ arn looks like.
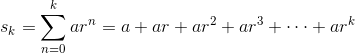
Notice that if you multiplied sk by another factor of the base r, then you would get:
![]()
The majority of the terms match with those of the original sk. So, if we subtracted the two expressions, most of the terms would cancel. After a bit of factoring and solving for the unknown sum, we can derive a useful formula.
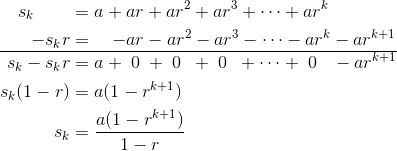
Next, we apply the limit to determine what happens in the infinite series. The key is that rx → 0 as x → ∞ so long as |r| < 1. On the other hand, if |r| ≥ 1, or r = ± 1, then rx diverges or there would be a nasty division by zero.
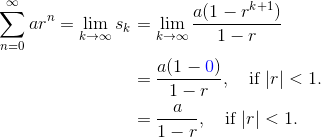
Examples from the AP Calculus BC Exam
A Simple Series
Find the sum of 2/3 – 2/9 + 2/27 – 2/81 + …
Solution
The common ratio is r = -1/3, and the initial term gives the coefficient: a = 2/3.
Because |r| = 1/3 < 1, the series converges. All that remains is to plug r and a into the sum formula.
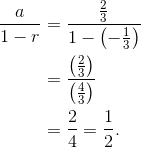
Therefore, the sum is exactly 1/2.
By the way, it’s always a good idea to check your work. If you add up just the first four terms, you get 2/3 – 2/9 + 2/27 – 2/81 = 0.4938, which is already pretty close to 0.5.
Rewriting the Terms
What is the value of 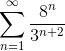 ?
?
Solution
This series is definitely geometric. However, in its current form it might be hard to see what is r and what is a. Let’s write out the first few terms of the series explicitly.
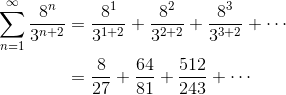
Now we can see that a = 8/27.
The common ratio is: (64/81) / (8/27) = 8/3 = r.
It’s tempting to jump straight to the sum formula, but if you did so, then you would get this one wrong. The trouble is that |r| ≥ 1, which implies that this series diverges. (There is no finite sum.)
Series of Functions
If 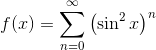 , then what is the value of f(π/3)?
, then what is the value of f(π/3)?
Solution
The geometric series formula works just the same when there are variables like x involved as well. Here, the common ratio (base) is r = sin2 x, which is always bounded by 1.
Then, once you get an explicit formula for f(x), you can plug in x = π/3.
0.999999… = 1???
One of my favorite demonstrations of the geometric series formula is in proving the paradoxical fact ![]() .
.
First of all, we have to write the decimal as a sum.
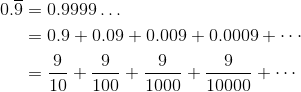
The last line shows that this sum is geometric, with a = 9/10 and common ratio r = 1/10. Because |r| = 1/10 < 1, we know that the sum must converge. Now use the formula to find the sum.
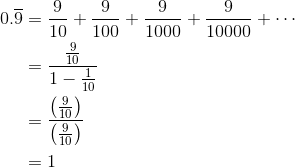
While this result may be very surprising at first, it’s definitely true. Indeed, it’s just as true as the fact that Achilles must eventually catch up to the Tortoise!

Summary
Let’s recap.
- A geometric series is the sum of powers of a constant base.
- Adjacent terms always have a constant ratio r.
- If |r| < 1, then the series converges to:

- If |r| ≥ 1, then the series diverges.
For more about series, you can check out the following review articles.





Leave a Reply