The ACT Math Test loves triangles! Out of all the ACT math topics tested, the triangle is the most commonly tested Geometric shape. The Pythagorean Theorem and the properties of right triangles are especially tested. The Pythagorean Theorem is a formula used to find the third side of a right triangle if you know the other two sides. Remember, it only works for a right triangle (a triangle with a 90-degree angle).
The Pythagorean Theorem can be represented as ![]() in which a and b are the two shorter sides and c is the hypotenuse (the name given to the side across from the 90-degree angle). To save time on the ACT Math Test, it helps to memorize and recognize the common Pythagorean triplets. These are common ratios between the sides that come up often in right triangles. The most common are 3:4:5 and 5:12:13. These ratios will also be true for any multiples of 3:4:5 and 5:12:13 such as 6:8:10 or 10:24:26.
in which a and b are the two shorter sides and c is the hypotenuse (the name given to the side across from the 90-degree angle). To save time on the ACT Math Test, it helps to memorize and recognize the common Pythagorean triplets. These are common ratios between the sides that come up often in right triangles. The most common are 3:4:5 and 5:12:13. These ratios will also be true for any multiples of 3:4:5 and 5:12:13 such as 6:8:10 or 10:24:26.
For example, if you are told a right triangle has a hypotenuse of 10 and one side with a length of 6, you can tell that the third side is 8. That’s because it must fit a 6:x:10 ratio, which if we divide by two becomes 3:(x/2):5. This looks a lot like 3:4:5, so x/2 = 4, and x = 8. Definitely a good time-saver!
There are also two right triangles that are very important to know called the special right triangles. These are so called because the ratio of their sides never changes. The first is a 30-60-90 triangle. Its sides will always be in a ratio of x: x√3 : 2x. The other special triangle is the 45-45-90 triangle. Its sides will always be in a ratio of x: x: x√2.
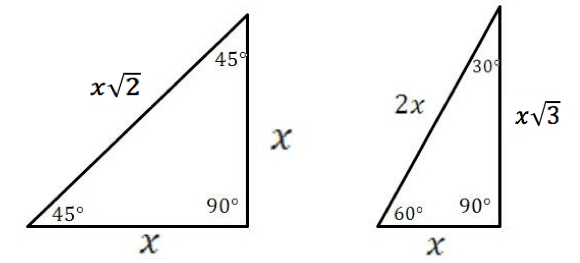
It’s important to remember that for the 30-60-90 triangle, the hypotenuse is the side that has the ratio of 2x. Don’t confuse it with the 45-45-90 ratio, and think that the x√3 should be there!
Here’s great question that illustrates how knowing these special right triangle ratios can be invaluable:
Which of the following sets of three numbers could be the side lengths, in yards, of a right triangle containing a 45° angle?

Here, even if we forgot the 45-45-90 ratios, we can eliminate any choice that doesn’t meet the Pythagorean theorem, since the question tells us we’re dealing with a right triangle.
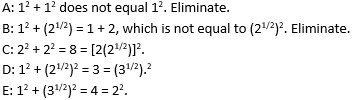
To choose between (C), (D), and (E), notice that a right triangle with one 45 degree angle must have another 45 degree angle. 180 – 90 – 45 = 45. This means that the triangle is isosceles, and the correct answer choice must contain two equal values. The correct answer is (C).






Leave a Reply