Remember, a complex number is very similar to a binomial. We’re dealing with imaginary and real numbers at the same time. We already took a look at addition and subtraction, so let’s move on to multiplication and division. These are a little trickier, but only division involves a skill you may not have used yet. Take a look!
Multiplication
Do you remember having to learn how to FOIL? You multiply the terms of a binomial or complex number in this order: First, Outer, Inner, Last. Let’s take a look at how to do it with a complex number.

That leaves us with this:
![]()
Now remember, 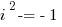 , as we already covered. So we get this:
, as we already covered. So we get this:

Division
All right, here’s where things get a little tricky, but stick with me. I promise, we’ll come out on the other side (mostly) unscathed.
Let’s say you had to divide 5 + 2i by 6 + 3i.

Now, remember, i is just another way of writing √-1. And, according to the ancient laws of math, we can’t have a radical in the denominator (or bottom part) of a fraction. So, it looks like we have to simplify in order to solve this problem.
Step One: Conjugate
In order to divide complex numbers, what you have to do is multiply by the complex conjugate of the denominator. I heard about half of you get sudden migraines there, but I promise, that’s not as complicated as it sounds. The complex conjugate is just the same exact denominator with one tiny change. Instead of 6 + 3i, we take 6 – 3i.
So our problem now looks like this:

Really, all we’re doing is multiplying by a fancy form of 1, so we’re not actually changing the problem; we’re just simplifying it.
Step Two: Multiply
It looks like we’re out of plastic wrap, which is okay, because all we need is FOIL. Yes, the good old First-Outer-Inner-Last method of multiplying binomials and complex numbers is back again. And this time, it’s personal.
Okay, not really. But let’s FOIL anyway. We’ll do the numerator first.

That leaves us with this:
![]()
And now, do the denominator the same way:

Step Three: Simplify
Here’s our problem so far:

We already know that 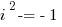 , so let’s change that in both the numerator and the denominator.
, so let’s change that in both the numerator and the denominator.

And now, combine like terms! Watch the magic!
Notice how the denominator suddenly doesn’t have any more i in it. We’ve fully simplified this problem! Woo-hoo! Take a nice deep breath, Magooshers! You’ve earned it.







Leave a Reply