Conquering Right Triangles & the Pythagorean Theorem on ACT Math – Part 2

If you’ve read Part 1 of the “Conquering Right Triangles…” series, you’re ready to rock some more challenging ACT Math questions with a quick “Triangles” quiz! Try each question on your own, then check your answer against the explanation!

Question #1: A right triangle with one length of 60 degrees has two leg lengths of x of and 2√3. If side 2√3 is across from the 60-degree angle, what is the measurement of x?

A) 2

B) 2√3

C) 4

D) 4√2

E) 4√3

Here it is a good example of how drawing the triangle can be vital to getting the correct answer on a right triangle question. A 30-60-90 triangle has a ratio of x: x√3: 2x. If 2√3 is across from the 60-degree angle, then x = 2. The correct answer is (A).

Question #2: If triangle ABC is a 30-60-90 right triangle, which of the following sets could represent triangle ABC’s side lengths?

A) 2, 2, 2

B) 2, 2, 2√2

C) 2, 2√2, 2√2

D) 2, 2√2, 2√3

E) 2, 2√3, 4

For each answer choice x = 2, so knowing that the ratio of a 30-60-90 is x: x√3 : 2x, we can plug x in to get: 2: 2√3 : 2(2) or 2: 2√3 : 4. The answer is (E).

Now let’s look at an example with the 45-45-90 triangle:

Question #3: Which of the following sets of three numbers could be the side lengths, in yards, of a right triangle containing a 45° angle?

Recall that a fractional exponent is just another way of expressing a root. We know the ratio for a 45-45-90 is x: x: x√2, which means two of the sides must be equal. That eliminates D and E. Out of the remaining choices, only (C) correctly expresses the ratio.

Sometimes the ACT Math Test will make triangles more challenging by disguising them within larger figures. Let’s look at an example for our final practice problem!

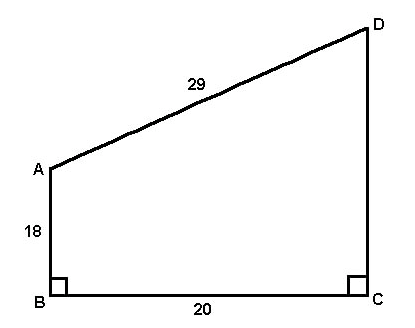
Question #4: What is the area of the trapezoid in the figure provided?

(A) 210

(B) 360

(C) 440

(D) 570

(E) 620

The trapezoid consists of two smaller shapes: a triangle and a rectangle. Draw a line from point A across this figure to form the two shapes.  Find the area of each shape and then add them together to find the area of the trapezoid.  Area of rectangle = length x width. Therefore, the area of the rectangle is 18×20 = 360

Therefore, area of the triangle = (¹/₂)(20)(21) = 210.  The total area of the trapezoid = 360+210 = 570, or (D).