
When you hear the word algebra, what comes to mind? Do you cringe at the thought of memorizing all the rules for dealing with equations? Do you freeze up when you see unknowns like x and y? Is asymptote a bad word to your ears? Well, this post on GRE Algebra will hopefully allay many of your fears and get you on the path to GRE math success!
![]() If you need a refresher on algebra, our Intro to GRE Algebra video tutorial can be the place to start!
If you need a refresher on algebra, our Intro to GRE Algebra video tutorial can be the place to start!
Table of Contents
- Algebraic Operations and Simplifying Expressions
- Rules of Exponents and Radicals
- Solving Equations in One Variable
- Linear/Quadratic Inequalities
- Solving Simultaneous Equations in Two Variables
- Word Problems and Applications
- Functions and Their Graphs
- Intercepts, Slope, and Other Topics in Coordinate Geometry
We’ll take a look at each topic listed above and work out a few GRE algebra practice questions along the way. Each example will be tagged as QC (quantitative comparison), MC (multiple choice), or NE (numeric entry). If you want to learn more about the question types on the GRE Math test, check out What Kind of Math is on the GRE?
Algebraic Operations and Simplifying Expressions
Algebraic expressions involve unknowns. When you simplify an algebraic expression, you need to keep a few basic rules in mind.
- Adding/subtracting: You can only combine like terms (same variable and exponent).
- Multiplying: Remember the distributive property!
Example (MC): What is the coefficient of 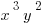 in below the expression?
in below the expression?
![3xy[( -4x^2y)-(7x^3y^2+x^2y)] 3xy[( -4x^2y)-(7x^3y^2+x^2y)]](https://magoosh.com/gre/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_37fe4303587832c8a9e53fa5ad6b473f.png)
(A) 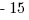
(B)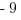
(C) 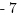
(D) 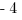
(E)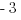
Answer: (A)
Explanation: First, break down the parentheses and combine like terms inside the brackets, and then distribute the 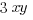 inside:
inside:
![3xy[ -4x^2y-7x^3y^2-x^2y] 3xy[ -4x^2y-7x^3y^2-x^2y]](https://magoosh.com/gre/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_1fd25e9e936a2c72d5f111e197e935bf.png)
![3xy[ -5x^2y-7x^3y^2] 3xy[ -5x^2y-7x^3y^2]](https://magoosh.com/gre/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_981_426db20b29623356429d71563a4be441.png)
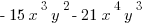
The first term has 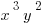 , so we just identify the first coefficient
, so we just identify the first coefficient 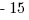 as our answer.
as our answer.
![]()
For more, check out our videos on the FOIL method and Factoring.
Rules of Exponents and Radicals
There are three basic rules of exponents:
- xaxb=xa+b
- xa/xb=xa-b
- (xa)b=xab
Together with the rule for converting radicals into exponents, every other property basically derives from these rules. For example: q√xp = xp/q
Example (MC): If 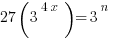 where
where  and
and 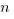 are integers, what is
are integers, what is 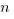 in terms of
in terms of  ?
?
(A) 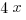
(B) 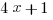
(C) 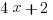
(D) 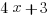
(E) 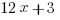
Answer: (D)
Explanation: The clue is that 27 is a power of 3.
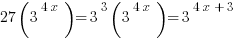
Therefore, if 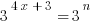 , then
, then 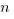 must be equal to
must be equal to 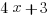 . For more on GRE exponents, review our Exponents Basics and Practice post.
. For more on GRE exponents, review our Exponents Basics and Practice post.
Solving Equations in One Variable
On the GRE, you may need to solve for an unknown in an equation with multiple variables.
Example (MC): Solve 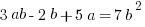 for
for 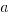 in terms of
in terms of 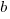 .
.
(A)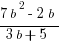
(B)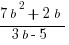
(C)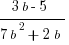
(D)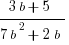
(E)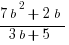
Answer: (E)
Explanation: Group, factor, and divide!
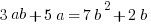
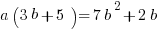
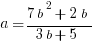
Linear/Quadratic Inequalities
Inequalities are used in mathematics to set up relationships of comparison. You’ll know you’re dealing with an inequality if you see one of these symbols: < > ≤ ≥
GRE math inequalities are typically of the linear variety, and so are easy to solve within a few steps. If a quadratic or another kind of expression shows up, then the analysis becomes trickier.
Example (QC) :
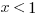
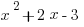 |
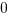 |
Answer: The relationship cannot be determined from the information given.
Explanation: QC problems are actually inequalities in disguise! Set up the inequality involving the two quantities to test whether Quantity A > Quantity B, and make your decision based on the answer.
x2+2x-3>0
(x-1)(x+3)>0
The roots x = 1, -3 are where the sign can change.
Plugging in sample points, you can see that the expression is positive for x < -3 and x > 1 and it’s negative for -3 < x < 1.
For example, x = -2, which is less than 1, will yield a negative result (-3), whereas x = -4, which is also less than 1, will yield a positive result (21).
Therefore, with only the given information, x<1 we cannot determine whether the quantity is positive or negative.
Solving Simultaneous Equations in Two Variables
When there are multiple equations in more than one variable, things can get tricky! There are a couple of trusted techniques to remember, such as substitution or elimination, which you can read about in Systems of Equations on the GRE.
Example (QC) :
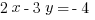
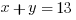
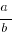 where where 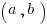 is a solution to the system. is a solution to the system. |
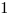 |
Answer: Quantity A is larger.
Explanation: Solve the system—we’ll use substitution for this one. The second equation can be rearranged to: 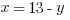 . Substitute that into the first equation and solve.
. Substitute that into the first equation and solve.
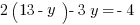
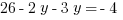
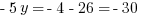
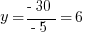
Then find  by back-substituting:
by back-substituting: 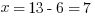 . Thus,
. Thus, 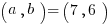 , and so
, and so ![]()
Word Problems and Applications
The dreaded word problems! What makes these questions so difficult? It’s probably because each word problem seems completely different from the next. Your task is to come up with an algebraic method for working out the solution, rather than just solving an equation that was given to you. Some problems require formulas that need to be memorized before test day.
Example (Numerical Entry): Terry wants to invest $2000. What annual simple interest rate would be required in order for Terry to have a balance of $3140 by the end of three years?
Answer: 19%
Explanation: Set up the simple interest formula, plug in, and solve for the unknown rate.
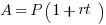
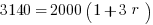
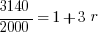
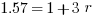
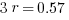
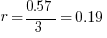
![]() For more explanation, try these helpful videos on Word Problems and Assigning Variables. And for some helpful hints on specific kinds of word problems, you might enjoy GRE Work Rate Problems and Distance Rate Time Formula Memorization Shortcut.
For more explanation, try these helpful videos on Word Problems and Assigning Variables. And for some helpful hints on specific kinds of word problems, you might enjoy GRE Work Rate Problems and Distance Rate Time Formula Memorization Shortcut.
Functions and Their Graphs
What is a function? It’s just a rule that tells you what to do with numbers. For example, the function 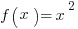 tells you to square any input (even if the input has variables). So
tells you to square any input (even if the input has variables). So 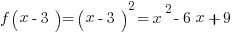 .
.
Functions can be graphed by plotting all of the 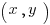 points where
points where 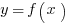 .
.
Example (MC): If the graph of the function 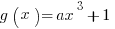 goes through the point
goes through the point 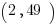 , what is the value of
, what is the value of 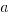 ?
?
(A) 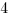
(B) 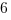
(C) 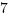
(D) 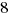
(E) 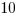
Answer: (B)
Explanation: Simply plug 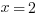 into the function:
into the function: 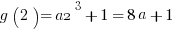 . We know
. We know 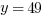 , so set equal and solve!
, so set equal and solve!
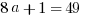
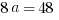
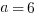
Sometimes, functions are given using strange symbols, so just be aware!
Intercepts, Slope, and Other Topics in Coordinate Geometry
![]() There’s a lot to know about coordinate geometry, but here’s the absolute #1 one tip: Know your slope-intercept form for lines (y=mx+b). Here’s a great video about Slope-Intercept Form!
There’s a lot to know about coordinate geometry, but here’s the absolute #1 one tip: Know your slope-intercept form for lines (y=mx+b). Here’s a great video about Slope-Intercept Form!
Example (NE): What is the 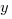 -coordinate where the line through
-coordinate where the line through 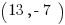 and
and 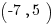 crosses the
crosses the 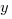 -axis?
-axis?
Answer: 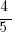
Explanation: Start by finding the slope.
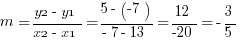
Then use the slope-intercept form, with one of the points plugged in to solve for the unknown 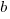 .
.
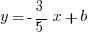
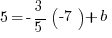
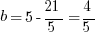
What’s Next?
Now that you’ve seen the GRE Algebra overview, you should check out the other math content areas for the GRE test:
- GRE Arithmetic: Overview and Practice
- GRE Geometry Formulas
- GRE Data Interpretation Practice Questions
Then try your hand at solving some more GRE Math Practice Questions to help prepare for GRE test day!





Leave a Reply