
GRE math questions cover a wide range of topics including arithmetic, algebra, geometry, and data interpretation. With so many areas to study, practice is the key to mastering the GRE math section.
Don’t worry—Magoosh is here to help! The GRE math practice questions in this post will help you identify which areas you need to work on and how well you’re prepared for the exam. Keep going for an in-depth look at 15 easy, medium, and hard GRE quantitative practice questions with answers and explanations. If you want to further assess your skill level in the Quant sections, head over to our GRE Quantitative Diagnostic Test!
GRE Math Practice Questions: What to Expect
For each of the five question types you’ll see in the GRE Quant section, we’ve included easy, medium, and hard questions for you to try. For every question in our product, Magoosh tracks how students perform on it so we can make sure each question is perfectly calibrated to mirror the real GRE!
Here’s how we categorize them:
Magoosh students (who are already determined to do well and have usually put in some study time!) answer “easy” questions correctly about 70% of the time. They answer “medium” questions right about 60% of the time, and “hard” questions right about 50% of the time.
Use the table below to jump to each practice question. If you’re returning to this post, skip to the answers and important takeaways.
GRE Quantitative Comparison Questions
Quantitative Comparison questions (also referred to as Quantitative Reasoning questions) don’t ask you to solve problems. Instead, they ask you to compare two quantities. On the official GRE, these could be equations, variables, angle measurements, or other quantities. Then, you choose the answer that best describes how they are related.
We’ve provided clickable radio buttons for you to select your answer as you go through these GRE math practice questions. This way, you can keep track of your answers and check your work at the end. However, please note that there’s no option to submit them!
Question 1
Difficulty: Easy
The revenue generated by Company X is divided between Doug and Moira in a 6 to 5 ratio respectively.
| Column A | Column B |
|---|---|
| Moira’s share when the revenue generated by Company X is $15,700 | $7,900 |
Question 2
Difficulty: Medium
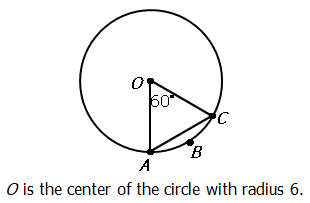
| Column A | Column B |
|---|---|
| Length of arc ABC | 6 |
Question 3
Difficulty: Hard
- The greatest prime factor of 144 is x
- The greatest prime factor of 96 is y
| Column A | Column B |
|---|---|
| x | y |
GRE Multiple-Choice Questions
For GRE multiple-choice questions, solve the problem on-screen and select the answer (one of five) that best answers it.
We’ve provided clickable radio buttons for you to select your answer as you go through these GRE math practice questions. This way, you can keep track of your answers and check your work at the end. However, please note that there’s no option to submit them!
Question 4
Difficulty: Easy
The price of a pair of sneakers was $80 for the last six months of last year. On January first, the price increased 20%. After the price increase, an employee bought these sneakers with a 10% employee discount. What price did the employee pay?
Question 5
Difficulty: Medium
If 6k2 + k = 2 and k > 0, then k must equal which of the following?
Question 6
Difficulty: Hard
In how many different ways can 3 identical green shirts and 3 identical red shirts be distributed among 6 children such that each child receives a shirt?
GRE Numeric Entry Questions
On GRE Numeric Entry questions, you solve a given problem by typing your answer into a box provided on-screen.
We’ve provided text boxes for you to type your answer as you go through these GRE math practice questions. This way, you can keep track of your answers and check your work at the end. However, please note that there’s no option to submit them!
Question 7
Difficulty: Easy
Dharik lives in a house on a straight street. For years, there have been 16 houses on his street to the right of his house and 17 houses on his street to the left of his house. Last year, 5 new houses were built on the same street even further to the left of those houses to the left of Dharik’s house. If these are the only houses on this street, how many houses are on this street?
Question 8
Difficulty: Medium
If 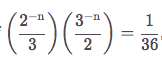 what is the value of n?
what is the value of n?
Question 9
Difficulty: Hard
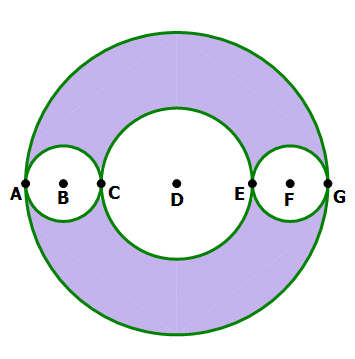
In the diagram, point D is the center of the medium-sized circle that passes through C and E, and it is also the center of the largest circle that passes through A and G. Each of the diameters of the small circles with centers B and F equals the radius of the medium-sized circle with center D. The shaded area is what fraction of the largest circle?
GRE Multiple-Answer Questions
If you encounter a question on GRE quantitative that appears to be multiple choice but does not specify that there is only one correct answer, you have found a multiple-answer question! Select all correct answer choices for this question type.
We’ve provided check boxes for you to mark your answer(s) as you go through these GRE math practice questions. This way, you can keep track of your answers and check your work at the end. However, please note that there’s no option to submit them!
Question 10
Difficulty: Easy
In a population of chickens, the average (arithmetic mean) weight is 6.3 pounds, and the standard deviation is 1.2 pounds. Which of the following weights (in pounds) are within 1.5 units of standard deviation of the mean?
Indicate all weights.
Question 11
Difficulty: Medium
If x > 0 which of the following expressions are equal to 3.6% of 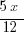 ?
?
Indicate all such expressions.
Question 12
Difficulty: Hard
A popular website requires users to create a password consisting of digits only. If no digit may be repeated and each password must be at least 9 digits long, how many passwords are possible?
GRE Data Interpretation Questions
GRE Data Interpretation questions are similar to multiple choice questions, with a twist: they ask you to look at graphics (primarily charts, graphs, and tables) and solve questions based on those.
We’ve provided clickable radio buttons for you to select your answer as you go through these GRE math practice questions. This way, you can keep track of your answers and check your work at the end. However, please note that there’s no option to submit them!
Question 13
Difficulty: Easy
| Animal | Percent |
|---|---|
| Lions | 32% |
| Leopards | 16% |
| Ocelots | 20% |
| Tigers | 8% |
| Bobcats | 24% |
If there are 44 leopards at the zoo, what is the zoo’s total animal population?
Question 14
Difficulty: Medium
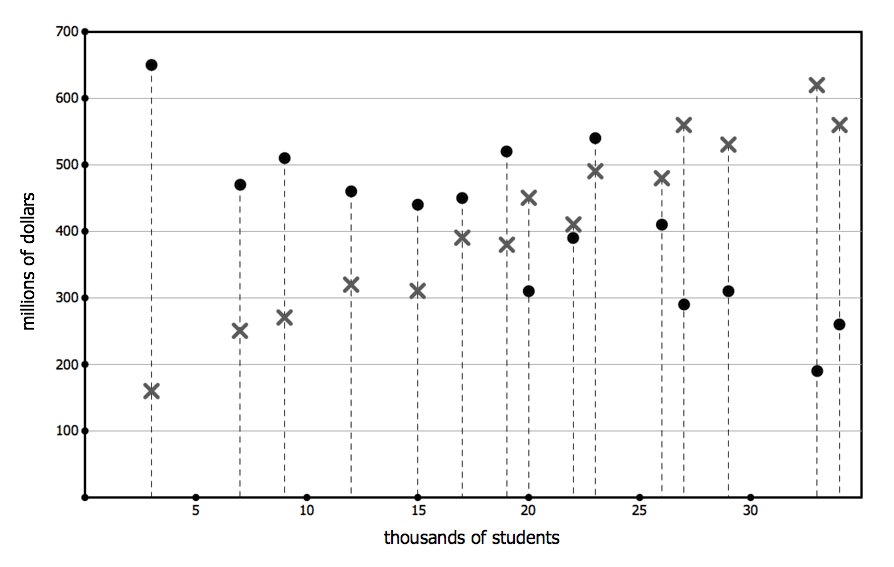
In the diagram above, each of fifteen private colleges is represented by a dot and an X on a vertical line. The X indicates the college’s annual income from tuition in 2008. The dot, above or below on the same dashed vertical line, indicates the college’s annual income in 2008 from investments such as endowments. The base of the vertical dashed line indicates the number of students at that college in 2008.
For how many colleges shown is the investment income in 2008 more than double the same college’s tuition income in 2008?
Question 15
Difficulty: Hard
The following chart shows the population of Jenkinsville and the number of televisions in the town through the middle of part of the 20th century.
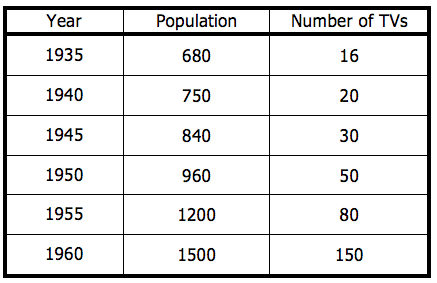
The ratio of people to televisions in Jenkinsville decreased by approximately what percent from 1955 to 1960?
Give your answer to the nearest integer percent and do not enter the percent sign.
GRE Math Practice Questions: Answers
GRE Quantitative Comparison Explanations
Question 1
Difficulty: Easy
Answer: The quantity in Column B is greater
Watch the video explanation here! Or, go back up to Question 1.
Question 2
Difficulty: Medium
Answer: The quantity in Column A is greater
Watch the video explanation here! Or, go back up to Question 2.
Question 3
Difficulty: Hard
Answer: The two quantities are equal
Watch the video explanation here! Or, go back up to Question 3.
GRE Multiple-Choice Explanations
Question 4
Difficulty: Easy
Answer: $86.40
Watch the video explanation here! Or, go back up to Question 4.
Question 5
Difficulty: Medium
Answer: 1/2
Watch the video explanation here! Or, go back up to Question 5.
Question 6
Difficulty: Hard
Answer: 20
Watch the video explanation here! Or, go back up to Question 6.
GRE Numeric Entry Explanations
Question 7
Difficulty: Easy
Answer: 39
Watch the video explanation here! Or, go back up to Question 7.
Question 8
Difficulty: Medium
Answer: 1
Watch the video explanation here! Or, go back up to Question 8.
Question 9
Difficulty: Hard
Answer: 5/8
Watch the video explanation here! Or, go back up to Question 9.
GRE Multiple-Answer Explanations
Question 10
Difficulty: Easy
Answers: 4.6, 5.1, 5.2, 6.9, 7.6, 7.7
Watch the video explanation here! Or, go back up to Question 10.
Question 11
Difficulty: Medium
Answers: x percent of 3/2; 3x/200
Watch the video explanation here! Or, go back up to Question 11.
Question 12
Difficulty: Hard
Answer: 2 × 10!
Watch the video explanation here! Or, go back up to Question 12.
GRE Data Interpretation Explanations
Question 13
Difficulty: Easy
Answer: 275
Watch the video explanation here! Or, go back up to Question 13.
Question 14
Difficulty: Medium
Answer: one
Watch the video explanation here! Or, go back up to Question 14.
Question 15
Difficulty: Hard
Answer: 33
Watch the video explanation here! Or, go back up to Question 15.
GRE Math Practice Questions: An Important Takeaway
How did your mini-GRE math practice test go? If you missed some (or even all) of the GRE math sample questions, don’t despair! You can still get the GRE score you want—and get into the graduate schools of your choice. With one big caveat…
When practicing GRE math problems, the key is to figure out why you answered questions incorrectly. Are you having trouble with the Numeric Entry question type? Are questions about geometry giving you the most issues? For a lot of students, it’s Quantitative Comparisons that prove tricky.
At first, this process can be frustrating. But remember, by forcing yourself to figure out the answer instead of immediately turning to an explanation during your GRE math practice, you will understand the problem at a deeper level and be less likely to miss a similar problem in the future. GRE math practice questions can help you get there. This is the best (and really the only) way to improve your score on the GRE. With enough GRE quantitative practice, you’ll get the score you want! And for more good habits that’ll help you get that high score, check out this video:
Special thank you to our contributor, Rachel Kapelke-Dale, for helping with this post!
Editor’s Note: This post was originally published in 2012 and has been updated for freshness, accuracy, and comprehensiveness.
Need more help?
Improve your GRE scores with Magoosh GRE, you can choose between a live cohorted class with an instructor (which includes all our lessons and practice questions) or access to the self-study option by itself.






Leave a Reply