Many quantitative questions have variables in both columns. While your first instinct may be to work algebraically, this strategy is not always best. Often the fastest way to a solution is by plugging in different values to see which column is greater.
Developing a sense of when to plug in and when to solve algebraically takes practice. Here are a few helpful guidelines when trying to determine which approach to use.
Work algebraically if the question is a polynomial
If you are dealing with a polynomial, simplify. Plugging in may require too much calculation. Instead, work with the familiar algebraic forms shown below:
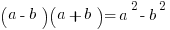
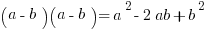
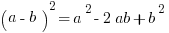
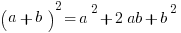
Now let’s take a look at a question.
| Column A | Column B |
|---|---|
 |
 |
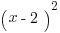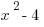- The quantity in Column A is greater
- The quantity in Column B is greater
- The two quantities are equal
- The relationship cannot be determined from the information given
In Quantitative Comparison we can make it so each side is equal. Then we can balance the equation, adding and subtracting, multiplying and dividing, where necessary.
First, note that 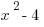can be factored into 
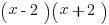. Now we can set both columns equal to each other:
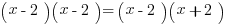
At this point we have to be careful. While algebra tells us to divide both sides by (x – 2), we need to be aware of the following: if x is between 0 and 2, (x-2) yields a negative. However, (x + 2) yields a positive, meaning (x – 2)(x + 2) gives us a negative. In this case (A) would be bigger.
However, if we divide each side by (x – 2) and solve we get the following:
DIVIDE EACH SIDE BY (x – 2)
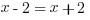
SUBTRACT ‘X’ FROM BOTH SIDES
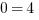
This hardly looks like a solution (in fact it looks like I forgot to go to grade school!). However, what this yields is the important insight: Column B is now 4 greater than Column A. Therefore, the answer is (D). Alternatively you could pick numbers, such as ‘0’ and ‘4’. Each gives us different answers, leading to the same conclusion: Answer (D).
If the question has variables, but there no polynomials, plug in values.
This advice pertains to variables that are not in polynomial form, as seen above. Here come up with easy numbers to plug in to see which values the columns yield.
0 > x > y > z > -1
| Column A | Column B |
|---|---|
 |
 |
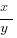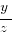- The quantity in Column A is greater
- The quantity in Column B is greater
- The two quantities are equal
- The relationship cannot be determined from the information given
.
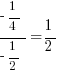
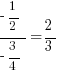It would be very nice if we could just stop here and choose answer (B). However, things are not so simple. When plugging in one set of numbers we will inevitably come up with one outcome. Once we’ve plugged in and come up with one answer, whether it is (A), (B), or (C), our job is to disprove that answer.
Can we make Column A larger than Column B? Well what if we plug in a values for x and y that are very close to one another.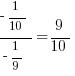 
. Now, for z we can plug in a value close to -1, say -8/9. This gives us 
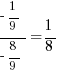. Now you can see (B) is much smaller. Therefore the answer is (D).
Takeaway
You should be adept at both algebra and plugging-in to efficiently—and accurately—answer a quantitative comparison question that contains variables. Typically it is best to simply check for polynomials before plugging in. To test out your skills, try these GRE math questions for practice!
Leave a Reply