For many, coordinate geometry is already a daunting concept. When a question dispenses with the graph all together, students can feel even more at a loss. If you fall into this group, do not despair. Here is a helpful guideline:
Do Not Always Draw the Graph
This advice may seem counterintuitive. After all, the problem didn’t provide a graph. Wouldn’t the first step be to graph the problem out?
Many coordinate geometry concepts sans graph are testing your conceptual thinking. Take the follow problem:
1. Which of the following lines do not contain coordinate points that are both negative?
Solution:
The slope formula is important – if the question is explicitly asking for the slope. What is often more important is knowing that a line with a negative slope – from left to right – slopes downward. A positive slope, unsurprisingly, slopes upward.
Think of it this way – start at a negative x-coordinate (say -2) of a line. If you were to place a ball on the line would roll down the line as it moved into positive territory for the x-coordinate? If so the line is negative, if not the line is positive.
For this problem, we are looking for a line that does not pass through the third quadrant – the quadrant in which x and y are both negative. Graph the point (-2, -2). That’s in the third quadrant.
Now here’s the big conceptual part – any line that slopes upwards will always pass through Quadrant III. Graph it if you have to – or simply imagine a line of infinite length sloping upwards. Anyway you try to do so there will always be the Third Quadrant waiting to claim a part of your line.
Now, imagine a downward sloping line. Is it also crossing through the third quadrant? Well, move the entire line to the right. At a certain point, your line will no longer be in the Third Quadrant. As long as that line crosses the y-axis at a positive value, it will never cross through the Third Quadrant.
Now you only need to find two things: a line that has a positive y-intercept and a negative slope. And that is much better than having to graph every one of the equations in answer choices A – E!
Only answer (C) x + y = 2, which can be re-written as y = -x + 2, has a negative slope (-1) and positive y-intercept (+2).
Takeaway
If a coordinate geometry question does not provide a graph, it is often testing conceptual thinking. So unless you are really desperate (which can happen on the GRE), and have time to spare, avoid graphing and think conceptually.
If you are unsure what to do, take a step back from the problem and ask yourself: will graphing this problem out take a long time? If the answer is yes, then there is very likely a much faster, no-graph approach.


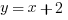
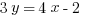
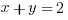
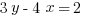
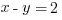




Leave a Reply