Below are the essentials to statistics on the GRE math section. These concepts are essential, so make sure you master them before walking into the test!
Mean
The mean is another way of saying average. To find the average add up the number of elements in the set and divide by the number of elements. For instance, let’s say I am counting the average number of push-ups my friends can do:
John: 10
Ray: 15
Cyrus: 22
Sue: 33
I find the total: 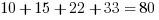 . I then divide by the number of elements. In this case, I have four friends.
. I then divide by the number of elements. In this case, I have four friends.
Another concept is range. The range of my friends’ push-ups above would be the difference between the greatest and the smallest: 33–10=23.
Mode
Set A: {2, 2, 2, 4, 5.5, 7, 7}
The number that shows up most in a list of numbers is the mode. Because the number two shows up the most frequently it is known as the mode. A list can have more than one mode, so if we were to add another 7 to the list above, 2 and 7 would both be the mode. However, if each number shows up only once, then we say that a set either has no mode or that every number in the set is a mode (for the GRE don’t really worry about this last part—I just want to make sure I dot my mathematical “i”s).
Standard Deviation
This one frightens many people, and understandably so. The good news is the GRE will rarely test you on finding the exact standard deviation on a list of numbers. (That fun task is reserved for stats 101 courses). Instead, the GRE wants you to have a sense of standard deviation.
Set A: 3, 4, 5, 6, 7
Set B: 2, 3, 5, 7, 8
Both sets have the same average. Notice how the spread in Set B is greater than that in Set A. Or, put another way, the numbers in Set A are clumped more closely together. The closer the spread (or the “clumpier”) the numbers, the lower the standard deviation.
The standard deviation for Set A is approximately 1.4 and that for Set B is approximately 2.3.
Distribution curve
This post is about normal distribution.
The above are intended as primer for statistics you’ll be seeing in GRE questions. In all likelihood they will probably get you to about the 50% level. However, if you are looking to score higher, esp. in the top 10%, then you will definitely want to practice with difficult questions. But don’t fret so much, as there aren’t so many statistics questions on the GRE. 🙂
Special Note:
To find out where geometry sits in the “big picture” of GRE Quant, and what other Quant concepts you should study, check out our post entitled:
What Kind of Math is on the GRE? Breakdown of Quant Concepts by Frequency






Leave a Reply