
The two Quantitative Sections will include Quantitative Comparison problems. Quantitative Comparison questions are integrated with the Problem Solving questions in two, 30-minute GRE math sections.
To learn more about this question type, we recommend reading the descriptions and strategies outlined by the ETS (the makers of the GRE).
From our perspective, they also want to see if you can
- understand the nature of a complex question format
- engage in logical and numerical analysis
- recall and apply mathematical principles in a problem-solving setting
- answer a series of mathematics-based problems under time constraints
Together with our analytical approach to this question-type we will provide
- problem recognition insights as the first step in analysis
- several time-saving strategies to guide you to the correct answer
- pre and post testing to assess progress
- lecture presentations plus numerous practice sets
- four interactive math tutorials for review of troublesome areas
On the actual exam the answer choices (A), (B), (C), and (D) will be activated to permit students to click on, then confirm their choice before moving on to the next problem.
The quantitative comparison problems are usually presented before the problem-solving questions which comprise a 20 problem (approximately) 30 minute set.
Directions: Each of the sample questions consists of two quantities, one in Column A and one in Column B. There may be additional information, centered above the two columns, that concerns one or both of the quantities. A symbol that appears in both columns represents the same thing in Column A as it does in Column B. You are to compare the quantity in Column A with the quantity in Column B and decide whether:
- Quantity A is greater.
- Quantity B is greater.
- The two quantities are equal.
- The relationship cannot be determined from the information given.
Example #1:
| Quantity A | Quantity B |
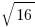 |
3.9 |
A. is the correct answer.
The square root of 16 (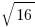 ) denotes the positive square root of 16 equals +4. Thus Quantity A is greater than Quantity B so A. is the correct answer.
) denotes the positive square root of 16 equals +4. Thus Quantity A is greater than Quantity B so A. is the correct answer.
Example #2:
| Quantity A | Quantity B |
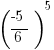 |
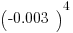 |
B. is the correct answer.
A negative value raised to an even number is always positive, whereas a negative value taken to an odd power will remain negative. Disregard the values with this problem and focus on the signs and powers. And there is no need to carry out the calculations. Since B. is positive, it is the larger value.
Example #3:
| Quantity A | Quantity B |
| The average of all the positive multiples of the integer 2 that are less than 10 | The fourth root of 625 |
C. is the correct answer. The average of the multiples of 2 that are less than 10 is 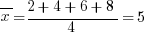 .
.
The fourth root of 625 is found by 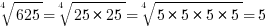
Example #4:
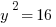
| Quantity A | Quantity B |
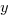 |
The smallest odd prime number |
D. is the correct answer.
Solve the given 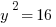 .
. 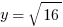 and
and 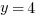 . Don’t confuse this problem with Example #1.
. Don’t confuse this problem with Example #1. 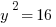 implies that either
implies that either 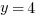 or
or 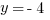 . A prime number is divisible by only two factors, 1 and itself. Thus, 1 is not a prime number but 2 is. Then, three is the smallest odd prime number. If
. A prime number is divisible by only two factors, 1 and itself. Thus, 1 is not a prime number but 2 is. Then, three is the smallest odd prime number. If 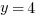 then A. would be the correct answer. But if
then A. would be the correct answer. But if 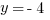 , then B. would be correct. The relationship cannot be determined, and D. is your choice.
, then B. would be correct. The relationship cannot be determined, and D. is your choice.






Leave a Reply