The following is a set of four GMAT Integrated Reasoning MSR questions. There are two information cards in this question. You are allowed to use a calculator. For the set of four, give yourself 10 minutes.
The cards
The questions
1. Player A initially draws three-of-a-kind and chooses not to discard at all on the discard round. Player B initially draws three-of-a-kind, discards the remaining two cards. For the following final card combinations of Player B, tell whether Player A outscores Player B.
2. Suppose player J draws two pair and chooses not to discard any cards. Suppose player K draws three-of-a-kind and choose not to discard any cards. Which of the following discard choices and final card combination would have a higher point value than player J’s hand but not than player K’s hand?
(A) discard 1 card, three of a kind
(B) discard 2 cards, flush
(C) discard 2 cards, straight
(D) discard 3 cards, full house
(E) discard 4 cards, full house
3. Player G received the following cards on the initial five-card draw: 2 of Clubs, 5 of Diamonds, 8 of Hearts, 8 of Spades, and King of Diamonds. Player G will choose to discard exactly two cards, the 2 of Clubs and 5 of Diamonds. Over all possible hands that could result, what is the range of the possible point values of Player G’s final hand?
(A) 588
(B) 598
(C) 1794
(D) 3588
(E) 3598
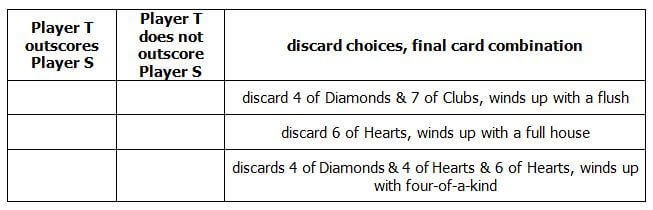
4. Suppose player S draws a straight on the first five-card draw and choose not to discard any cards. Player T initially draws the following five cards: 4 of Diamonds, 4 of Hearts, 6 of Hearts, 7 of Hearts, 7 of Clubs. Which of Player T’s discard choices and final results will outscore Player S?
Answers
1. Three-of-a-kind = A outscores B
Full House = A does not outscore B
Four-of-a-kind = A does not outscore B
2. C
3. B
4. first row = T does not outscore S
second row = T outscores S
third row = T outscores S
Explanations
1) Player A draw three-of-a-kind (worth 60 points), and does not discard, so A’s hand is worth 60 points. In all three cases, B discards two cards, for a reducing factor of 1/6.
(a) B’s final hand = three-of-a-kind, which is (60)*(1/6) = 10 points. A outscores B.
(b) B’s final hand = Full House, which is (720)*(1/6) = 120 points. A does not outscore B.
(c) B’s final hand = Four-of-a-kind, which is (3600)*(1/6) = 600 points. A does not outscore B.
It wasn’t relevant in any of these scenarios, but notice the exact wording — if A and B were tied, the answer would be “A does not outscore B.”
2) Player J, with two pair and no discards, has 36 points. Player K, with three-of-a-kind and no discards, has 60 points. We want a combination worth more than 30 points but less than 60 points.
(A) discard 1 card, three of a kind = (60)*(1/2) = 30. Less than 36, no good.
(B) discard 2 cards, flush = (540)*(1/6) = 90. Higher than 60, no good.
(C) discard 2 cards, straight = (300)*(1/6) = 50. This could work.
(D) discard 3 cards, full house = (720)*(1/10) = 72. Higher than 60, no good.
(E) discard 4 cards, full house = (720)*(1/60) = 12. Less than 36, no good.
(C) is the only hand & discard combination that is in the required range.
3) The five original cards in Player G’s hand are: 2 of Clubs, 5 of Diamonds, 8 of Hearts, 8 of Spades, and King of Diamonds. Player G discards the 2 of Clubs and 5 of Diamonds, leaving two 8’s and a king. We know that Player G’s reducing factor for this hand will be 1/6.
The highest possible hand would be four-of-a-kind, in the unlikely scenario that G picked up the other two 8’s. That would result in (3600)*(1/6) = 600 points, the maximum.
The lowest possible hand would be if G picks up garbage and just has the two 8’s. That would result in (12)*(1/6) = 2 points, the minimum.
The range of any set is the max minus the min. Range = 600 – 2 = 598.
Answer = (B)
4) Player S’s hand is worth 300 points. That’s fixed. Now, we have to compare T to that 300 point total. discard 4 of Diamonds & 7 of Clubs, winds up with a flush
Scenario #1: discard 4 of Diamonds & 7 of Clubs, winds up with a flush. Flush is worth 540, times the reducing factor of 1/6, for a point value of 540*(1/6) = 90, which is less than S. Player T does not outscore player S.
Scenario #2: discard 6 of Hearts, winds up with a full house. Full house is worth 720, times reducing factor of 1/2, for a point value of 720*(1/2) = 360, which beats S. T outscores S.
Scenario #3: discards 4 of Diamonds & 4 of Hearts & 6 of Hearts, winds up with four-of-a-kind. Four-of-a-kind is worth 3600, times a reducing factor of (1/10), for a point value of 3600*(1/10) = 360, which beats S. T outscores S.









Leave a Reply