In the following problems, remember: no calculator! Difficulty levels range from medium to hard.
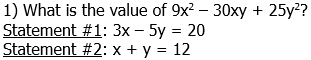
2) Maggie is 15 years older than Bobby. How old is Bobby?
Statement #1: In 3 years, Maggie’s age will be 50% larger than Bobby’s age.
Statement #2: Years ago, when Maggie was 25 years old, Bobby was 10 years old.
3) By abc we denote a three digit number with digits a, b, and c. Is abc divisible by 3?
Statement #1: The product of (a) times (b) is a number divisible by 3
Statement #2: c = 3
5) The ratio of underclassmen to upperclassmen in a particular school is 4:5. How many underclassmen are there?
Statement #1: If the number of upperclassmen increased by 20%, then underclassmen would constitute 40% of this larger student body.
Statement #2: If 10 more underclassmen joined the school, the new ratio of underclassmen to upperclassmen would be 9:10.
6) If k is a positive integer, is k prime?
Statement #1: k has fewer than four positive factors
Statement #2: 150 ≤ k ≤ 200
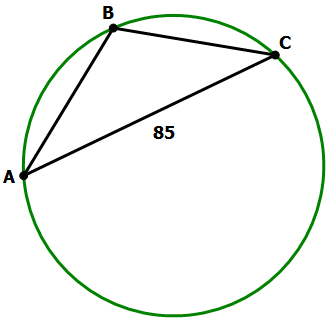
7) In the circle above, chord AC = 85. What is the area of the circle?
Statement #1: Angle ABC = 90°
Statement #2: AB = 51 and BC = 68
8) An oddly shaped die has N sides, numbered from 1 to N, that are equally likely to appear on a throw. Let P be the probability that at least one “1” appears in two throws. Is P < (1/5)?
Statement #1: N is a prime number
Statement #2: N > 5
9) Set S consists of all the positive multiples of 5 that are less than K, and K is a positive integer not divisible by 5. The mean of Set S is not divisible by 5. Let N be the number of members of the set. N is not divisible by 5. What does N equal?
Statement #1: N < 52
Statement #2: K/5 > 48
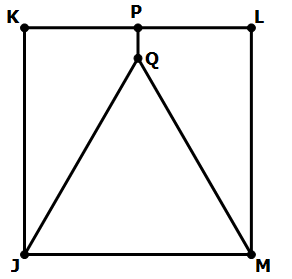
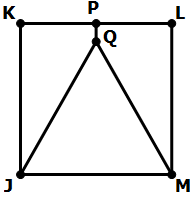
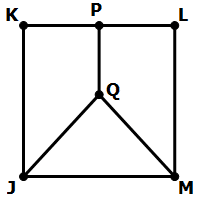
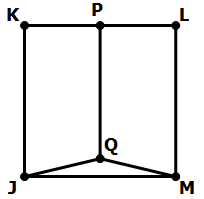
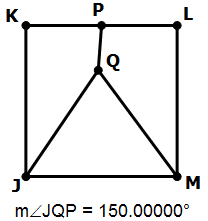
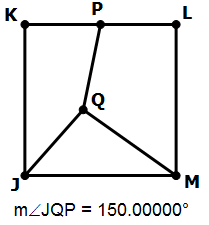
11) In the diagram, JKLM is a square, and P is the midpoint of KL. Is JQM an equilateral triangle?
Statement #1: Angle KPQ = 90°
Statement #2: Angle JQP = 150°
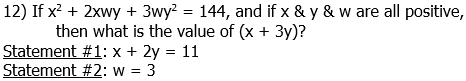
13) If n is a positive integer, does n have four or more distinct factors?
Statement #1: n is not prime
Statement #2: 150 ≤ n < 200
14) The numbers D, N, and P are positive integers, such that D < N, and N is not a power of D. Is D a prime number?
Statement #1: N has exactly four factors, and D is a factor of N
Statement #2: D = (3^P) + 2
Data Sufficiency on the GMAT
If you are new to the GMAT, then know that these questions are on the hard side. If you are just getting familiar with this question type, please see this blog:
GMAT Data Sufficiency Strategies
Here are more blogs of practice DS questions:
GMAT Sample Data Sufficiency Practice Questions
GMAT Data Sufficiency Practice Questions on Probability
Below are the answers, followed by full solutions. If you have any takeaways after reading the solutions, please let us know in the comments section about what you have learned!
Answers
1) A
2) A
3) E
4) A
5) B
6) E
7) D
8) E
9) C
10) B
11) C
12) B
13) E
14) C
Solutions
1) First of all, it is very helpful to notice that the expression given in the prompt is the Square of a Difference.
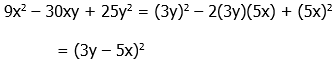
Thus, if we knew the value of (3y – 5x), we could find the value of the given expression.
Statement #1 gives us exactly the value we need. This statement, alone and by itself, is sufficient.
Statement #2 gives us the value for another expression, x + y = 12. There is no way, starting from this, to find the value of (3y – 5x). Therefore, this statement, alone and by itself, is not sufficient.
Answer = (A)
2) Let M = Maggie’s age right now, and let B = Bobby’s age right now. The prompt gives us the equation M = B + 15.
Statement #1 gives us a second equation, (M + 3) = 1.5*(B + 3). Notice that I used a multiplier for the percent increase. With this equation and the prompt equation, we have two equations with two unknowns, so we can solve for the values of M & B. We don’t need to perform those calculations: it is enough to know that we could. This statement, alone and by itself, is sufficient.
Statement #2 is already obvious from the prompt. If Maggie is 15 years older than Bobby, then when Maggie was 25, Bobby would have had to have been 10. There’s no surprise there. We are given absolutely no indication when these people were these ages, so this doesn’t help us at all. This statement, alone and by itself, is not sufficient.
Answer = (A)
3) Remember, the divisibility rule: if the sum of all the digits in a large number is divisible by 3, then the number itself is divisible by three.
The problem with statement #1, for any given values of a & b that work, the one’s digit, c, could be anything. For example, a = 1, and b = 3 satisfy this condition, so that would be all the numbers in the 130’s: {130, 131, 13, 133, 134, 135, 136, 137, 138, 139}. Clearly, some of these are divisible by 3, namely {132, 135, 138} and the others aren’t. This statement allows for multiple answers, so this statement, alone and by itself, is not sufficient.
The problem with statement #2 is that we now know the one’s digit, but the other two digits could be anything. Think about the first few possible numbers of this form: {103, 113, 123, 133, 143, 153, 163, 173, 183, 193, 203}. Of those, only (123, 153, 183) are divisible by three, and the others aren’t. In fact, you would be expected to know this, but as it happens, {103, 163, 173, 193} are prime numbers, not divisible by anything! This statement also allows for multiple answers, so this statement, alone and by itself, is not sufficient.
Combined statements: now, we have to obey both constraints. One number that obeys both constraints is 133, which is not divisible by 3. Another number that obeys both constraints is 333, which is divisible by 3. Even with both statements in place, we can find numbers that produce either a “yes” or a “no” to the prompt. Even together, the statements are not sufficient.
Answer = (E)
4) It is helpful to find the equivalent forms of the expression given.
Statement #1 is close to one of the form for this.
Now, multiply by a negative sign to reverse the order of the subtraction.
This statement has allowed us to arrive at the value of the expression. This statement, alone and by itself, is sufficient.
The Statement #2 expression cannot be simplified or factored. There is no easy way to relate this the expression in the prompt. Because we have only one equation, we can’t solve for the value of either of the variables. This statement, alone and by itself, is not sufficient.
Answer = (A)
5) We are given “ratio information” and we want actual numbers. To get counts, actual numbers of people, we need something besides more ratio information.
Statement #1 just gives us more “ratio information,” so we can’t solve for counts. This statement, alone and by itself, is not sufficient.
Statement #2 gives us some actual counts. Let N and P represent the current underclassmen and upperclassmen, respectively, in the school. We know N/P = 4/5 from the prompt. From this statement, we know (N + 10)/P = 9/10. Together, we have two equations for two unknowns, so we could solve for the values of N & P. This statement, alone and by itself, is sufficient.
Answer = (B)
6) Remember that every prime number has just two factors:
(a) 1, which is a factor of all integers
(b) the prime number itself (every number is a factor of itself)
Statement #1 tells us that k has fewer than four factors. It could be prime number with just two factors. Most non-prime numbers have 4+ factors. The exception, though, are the squares of prime numbers, which have 3 factors. For example, the factors of 9 are {1, 3, 9}; the factors of 25 are {1, 5, 25}. According to this statement, k could be prime, or it could be one of these numbers. We cannot give a definitive answer to the prompt question. This statement, alone and by itself, is not sufficient.
Statement #2 just gives a range, and k could be anything in that range. There are some prime numbers in that range, and many numbers that aren’t prime. This statement doesn’t help much at all. This statement, alone and by itself, is not sufficient.
Combined statements: now, we know that k is a number with fewer than four factors between 150 and 200. (Neither of those endpoints are allowed, because both 150 and 200 have many more than 4 factors!) Well, all the prime numbers in that range would be possible, and they would give a “yes” answer to the prompt. Unfortunately, one square of a prime number also falls in that range. The square of 13 is 169, so 169 has three factors: {1, 13, 169}. If k = 169, then both statements are satisfied, but the answer to the prompt is “no.” We still cannot give a definitive answer to the prompt question. Even combined, the statements are not sufficient.
Answer = (E)
7) If we know chord AC were a diameter, then we would divide by 2 to find the radius. Once we know the radius, we could find the area. Furthermore, we would know that AC were a diameter if the angle at B were a right angle, because an inscribed angle of 90° always intersects a semicircular arc.
Statement #1 simply tells us that the angle at B is 90°, so we are done! This statement, alone and by itself, is sufficient.
Statement #2 gives us the other two sides of triangle ABC, we now we know we have a {51, 68, 85} triangle. If these three sides satisfy the Pythagorean Theorem, then the triangle would be a right triangle, and the angle at B would be 90°. Well, it would be HUGE mistake to square these numbers as is and try to do anything with the results! Instead, can we factor out a common factor? Well, 51 = 3*17. Also, notice that 85 = 5*17. This makes us suspicious, and it turns out, 68 = 4*17. This is simply the good old 3-4-5 triangle, with everything multiplied by 17. Of course, this is a right triangle, so the angle at B is 90°. This statement, alone and by itself, is sufficient.
Answer = (D)
8) First of all, if the N sides are equally likely, the probability of getting “1” on a single throw, or any particular side on a single throw, is 1/N. The probability of not getting “1” on a single throw, or not getting any particular side, is (1 – 1/N) = (N – 1)/N.
For relatively low values of N, then getting “1” is relatively more likely, and getting something else is relatively less likely. As N gets bigger, the probability of getting “1” on a single throw decreases, and the probability of getting something else increase.
What really makes the difference in this probability is the size of N. This is an at least probability, so we calculate the probability of getting something other than one on two consecutive throws, and then subtract this from 1.
Statement #1: this statement is not very helpful. If N = 2, then essentially, the “two-sided die” is a coin, and if H = 1, then the probability of not getting a “1” is (1/2). The probability of not getting a “1” on two consecutive throws is (1/4). That’s the probability of getting no “1” on two throws. We subtract this from one to get the probability of at least one “1”: P = (3/4), which greater than 1/5. Answer to the prompt = “no.”
But, suppose N is larger. For easy of calculation, I will pick N = 15, even though 15 is not prime. If N = 15 produces a probability less than 1/5, then so will any prime number greater than 15.
If N = 15, then the probability of not getting a “1” on a single throw is 14/15. The probability of not getting a “1” on two consecutive throws is this squared, 196/225. If this is more than 4/5, then subtracting it from one will be less than 1/5. Well, 225/5 = 45, and 45 times 4 is 180. Thus, (180/225) = (4/5), and (196/225) > (4/5). Subtracting this from one will produce a probability less than 1/5. Answer to the prompt = “yes.”
This statement is consistent with different answers to the prompt question, so it does not lead to a definitive answer. This statement, alone and by itself, is not sufficient.
Statement #2: We have already seen that N = 15, or any number larger than that, produces a “yes” answer to the prompt. Is it possible to produce a “no” answer to with a value of N greater than 5?
I will use N = 7. The probability of not getting a “1” on a single throw is 6/7. The probability of not getting a “1” on two consecutive throws is this squared, 36/49. If this is less than 4/5, then subtracting it from one will be more than 1/5.
Well, clearly, 36/45 = 4/5, and making the denominator larger makes a fraction smaller, so
4/5 = 36/45 > 36/49. So, this fraction is less than 4/5, so subtracting it from one will result in a probability that is greater than 1/5. This gives a “no” answer to the prompt.
This statement is consistent with different answers to the prompt question, so it does not lead to a definitive answer. This statement, alone and by itself, is not sufficient.
Combined statements: As we saw in the previous statements, the prime number N = 7 gives a “no” answer, and the non-prime N = 15 gives a “yes” answer, which implies that any prime number greater than 15 (such as 17, 19, 23, etc.) would also give a “yes” answer. Different answers are possible even with the constraints of both statements. Together, both statements are still not sufficient.
Answer = (E)
9) This is a tricky problem, because there are several constraints in the problem. first of all, the number of members is N, so the numbers in the set go from 5 to 5N. The integer K has the quality that 5N < K < (5N + 5), because K is bigger than the biggest member of the set, but 5N has to be the largest multiple of 5 less than K.
We know that the mean of the set is not divisible by 5, and this is important. For an evenly spaced set, the mean & median are identical. If there were an odd number of members, the mean & median would simply be the middle number on the list, and this of course would be some multiple of 5. The fact that mean & median is not divisible by 5 necessarily means that there must be an even number of members on the list. This way, the mean & median would be the average of the middle two numbers, which would be a non-integer, certainly not an integer divisible by 5. Therefore, N is an even number.
Finally, we are also told that N itself is not divisible by 5—an odd constraint that may be relevant.
Statement #1: Here, N could be any even number less than 52, as long as it’s not divisible by 5. It could be {48, 46, 44, 42, 38, ….} Multiple possibilities. This statement, alone and by itself, is not sufficient.
Statement #2: The statement tells us that K > 5*48, so it could be that N = 48, so that K would be between 5(48) and 5*(49). That’s a possibility, or N could be any larger even number that is not divisible by 5. N could be {48, 52, 54, 56, 68, 62, …} Again, multiple possibilities. This statement, alone and by itself, is not sufficient.
Combined statements: with both constraints, the only possible value if N = 48. The statements together are sufficient.
Answer = (C)
10) This is a very tricky fraction with quadratics. We know that the lead coefficient, the coefficient of x-squared, is positive, so this is an “upward-facing” parabola, curved side pointing down and “arms” going up.
We can compute that at x = 0, y = +5/12, a positive number. At x = 1, we get
At both x = 0 and x = 1, the output is positive. If a = 1 is the coefficient of x-squared, and ( – 4/3) is the coefficient of x, then the line of symmetry of the parabola is given by
The vertex, the lowest point on the parabola, would be at that position. The y-value there would be:
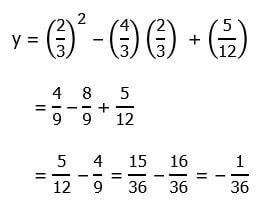
At x = 2/3, there is a vertex with a small negative y-value, but the parabola curves up, and by the time it gets to x = 0 or x = 1, it’s already positive and above the x-axis. OK, now we can look at the statements.
Statement #1: 0 ≤ x
Well, if x = 1, then we get a “no” answer, but if x = 2/3, then we get a “yes” answer. Two different answers to the prompt are possible. This statement, alone and by itself, is not sufficient.
Statement #2: x is an integer
This is interesting and subtle. We need to think about the shape of a parabola. This parabola is negative at x = 2/3 and the immediate vicinity, but by the time we get over to either adjacent integer, x = 0 or x = 1, the parabola is already positive.
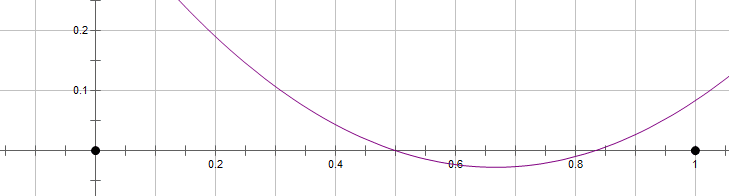
Once a parabola is going up, it keeps going, so for any integer to the left of x = 0, or any integer to the right of x = 1, it also will be positive. It is positive for every integer value. That means, we can give a definitive answer of “no” to the prompt question. Because we were able to give a definitive answer, this statement, alone and by itself, is sufficient.
Answer = (B)
11) First of all, clearly if we knew that that JQM is equilateral, then we could know that ÐKPQ = 90° and that ÐJQP = 150°. That much is clear. An equilateral triangle is consistent with the statements, but the question is, does either statement or do both of them necessitate that JQM be equilateral?
Statement #1: ÐKPQ = 90°
This statement guarantees that Q is directly below P, so that PQ lies on the vertical midline of the square. This guarantees that JQM is isosceles, but Q could be at any height.
This statement guarantees that JQM is isosceles. It may or may not be equilateral. This statement, alone and by itself, is not sufficient.
Statement #2: ÐJQP = 150°
Now, that obtuse angle is fixed, but we don’t know whether Q is still on that vertical midline. This could be the case in which JQM is equilateral, or it could be entirely asymmetrical.
With the restriction of this statement, it could be true that triangle JQM is equilateral, but as in these diagram, JQM might be completely asymmetrical. We can’t give a definitive answer. This statement, alone and by itself, is not sufficient.
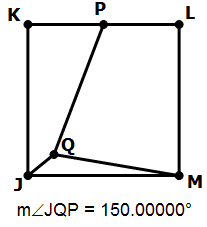
Combined statements: ÐKPQ = 90° & ÐJQP = 150°
The first statement tells us that PQ is on the midline, and that JQM must be isosceles. The entire diagram is symmetrical over this vertical midline. This means, if ÐJQP = 150°, then ÐMQP = 150° as well, and because the angles around point Q must add up to 360°, this means that ÐJQM must equal 60°. Well, any isosceles with one 60° angle must be equilateral. We absolute know that triangle JQM must be isosceles now. This is definitive. The statements together are sufficient.
Answer = (C)
12) We have one equation and three variables. Normally, we would need three equations to solve for the values of the individual variables. Here, though, we are asked to find the value of an expression, and in questions of this sort, often we can find the value of the expression without finding the individual variables. We need (x + 3y)
Statement #1: x + 2y = 11
Well, this gives us the value of another expression, and if we knew the value of y, we could simply add that to this expression to get the value of (x + 3y). The problem is: this would require us to solve for the individual variables, and we have only two equations for three variables. For example, we could solve this for x, x = 11 – 2y, and plug this into the prompt equation to eliminate x, but that would still leave us with one equation with both y and w as unknowns. One equation, two unknowns. We cannot solve for anything with this information. This statement, alone and by itself, is not sufficient.
Statement #2: w = 3
If we plug this into the prompt equation, we get:
This is the square of a sum, because it fits the pattern:
where a = x, and b = 3y. This means:
Normally, when we take a square root, we would have to consider the ± sign. Here, though, we are guaranteed that all three numbers, x & y & w, are positive, so the sum (x + 3y) would have to be positive. Thus, we can take a square root and be sure the answer will be positive.
x + 3y = 12
This statement lead directly to a numerical answer to the prompt question. This statement, alone and by itself, is sufficient.
Answer = (B)
13) Keep in mind, a prime number is number with only two factors, 1 and itself. All positive numbers with only two positive factors are prime numbers.
If we multiple one prime by another prime, say 2*5 = 10, then we get four factors, {1, 2, 5, 10}. Any product of two different primes has four factors. If one of the numbers we multiply is not prime, then it already has more than two factors of its own, and so the resultant product will have many more than 4 factors. It would seem that non-prime numbers have to have at least 4 factors.
The one exception is: squares of prime numbers. Consider what happens when we square 5: we get 25, and the factors of 25 are {1, 5, 25}. The square of a prime number is not prime, and it has three factors.
Statement #1: n is not prime
Well, if n is not prime, n could be 24 or 25. The first, 24, has factors {1, 2, 3, 4, 6, 8, 12, 24}—eight factors, so the answer to the prompt question is “yes.” Meanwhile, 25 has three factors, so the answer to the prompt question is “no.” Two different answers to the prompt are possible. This statement, alone and by itself, is not sufficient.
Statement #2: 150 ≤ n < 200
Clearly, many of the numbers in that range will have more than 4 factors, and the answer to the prompt is “yes.” But here, n could be prime, and there must be some prime numbers in that range. You don’t need to know this, but the prime numbers in this range are {151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199}. If n were any of these numbers, n would have only two factors, and the answer to the prompt question would be “no.” Two different answers to the prompt are possible. This statement, alone and by itself, is not sufficient.
Combined statements:
Now, n must be in the 150 to 200 range, and all prime numbers are excluded. As note, most of the numbers in this range will have a large number of factors, so for almost all of them, the answer to the prompt question is “yes.” The trouble is: there one number in this range that is the square of a prime number. The square of 13 is 169, so the factors of 169 are {1, 13, 169}. Since this is the square of a prime, it has exactly three factors. This gives a “no” answer to the prompt question. Even with combined statements, we still can get two different answers. Even combined, the statements are not sufficient.
Answer = (E)
14) This is a tricky one.
Statement #1: two kinds of numbers have exactly four factors: (a) products of two distinct prime numbers, and (b) cubes of prime numbers.
The product of two distinct prime numbers S and T would have factors {1, S, T, ST}. For example, the factors of 10 are (1, 2, 5, 10), and the factors of 21 are {1, 3, 7, 21}.
The cube of a prime number S would have as factors 1, S, S squared, and S cubed. For example, 8 has factors {1, 2, 4, 8} and 27 has factors {1, 3, 9, 27}.
We know N is not a power of D, so the second case is excluded. N must be the product of two distinct prime numbers. We know D < N, so of the four factors, D can’t be the product of the two prime numbers. D could be either of the prime number factors, or D could be 1, which is not a prime number. Because D could either be a prime number or 1, we cannot give a definitive answer to the question. This statement, alone and by itself, is not sufficient.
Statement #2: this is tricky. The first few plug-ins seem to reveal a pattern.

Even if you sense a pattern, it’s important to remember that plugging in numbers alone is never enough to establish that a DS statement is sufficient. Here, if we persevered to one more plug-in, we would find the one that breaks the pattern.
![]()
That gives another answer to the prompt, so we know this statement is not sufficient.
To avoid a lot of plugging in, it’s also very good to know that in mathematics, prime numbers are notorious for not following any easy pattern. It is impossible to produce an algebraic formula that will always produce prime numbers. In fact, this is more than you need to know, but the hardest unsolved question in higher mathematics, the Riemann Hypothesis, concerns the pattern of prime numbers; mathematicians have been working on this since 1859, and no one has proven it yet. Suffice to say that no one-line algebraic formula is going to unlock the mystery of prime numbers!
Combined statements: according to the information in statement #1, either D = 1 or D is a prime number. Well, statement #2 excludes the possibility that D = 1, because that number cannot be written as two more than a power of 3. Therefore, D must be a prime number. We have a definitive answer to the prompt question. Combined, the statements are sufficient.
Answer = (C)

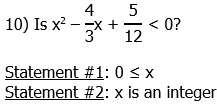

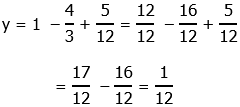
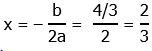
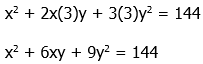



Leave a Reply