Using Diagrams to Solve GMAT Rate Problems: Part 2

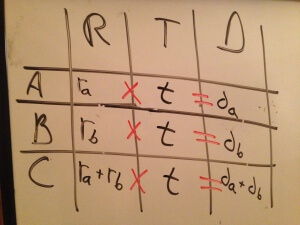
In Part 1 we used what is called an RTD table to solve a fairly typical rate problem. Today I want to revisit the problem in Part 1 to make a simple point:
 

There’s more than one correct way to use the table.

If you keep in mind a few simple truth about the RTD table and it’s application to simultaneous travel problems, your correct approach might look different than my correct approach, but we should both get the same right answer. If we also keep the number of variables to a minimum, we should get that right answer very efficiently.

Here are those few simple truths:

• If two travelers are moving simultaneously in opposite directions (whether toward each other or apart), add their rates. That means the R value in the bottom row should be the sum of the values above it.
• If two travelers are moving simultaneously in opposite directions (whether toward each other or apart), add their distances. That means the D value in the bottom row should be the sum of the values above it.
• If two travelers are traveling simultaneously, use the same value for T in all the rows.

 

So what might an alternative use of the RTD table look like?

Let’s suppose that we started as we did in Part 1, by circling the cell for whose value we’re solving, and by recording the time (2/3 of an hour), total distance (100 miles) and the rates for the two trains (r for X and r-30 for Y).

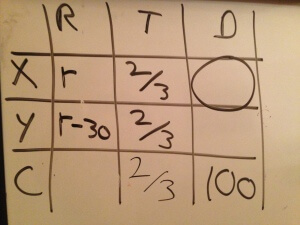
For last post’s solution we added r and r-30 to get a combined rate of 2r-30. That’s probably the easiest way to approach this, but suppose that instead of completing the R column, we instead completed the bottom, “combined” row.

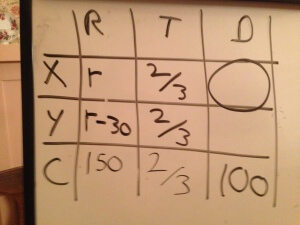
What we did there was to divide the combined distance (100) by the time (2/3) to get the combined rate (100/(2/3) or 150). Since the rates must sum to the combined rate, we can now solve for r using the equation,

r+(r-30)=150
2r-30=150
2r=180
r=90

As in Part 1, we still have one more step, to solve for (2/3)r=60.

 

Here’s another fine alternative:

Part 1 and today’s Part 2 both I represented X’s rate as r, just because we needed to eventually solve for X’s distance. Might as well keep X’s row simple, right? But notice that we still would have got the same answer if we’d called Y’s rate r, called X’s rate r+30, and solved for (2/3)( r+30).

One table consistent with that choice would look like this:

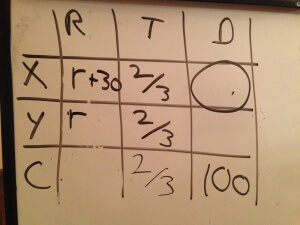
Add the rates to complete the first column.

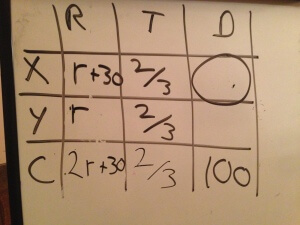
Using the formula DR=T with the bottom row yields,
(2r+30)(2/3)=100
(4r/3)+20=100
(4r/3)=80
4r=240
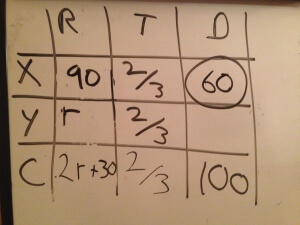
r=60

Substitute 60 for r in the top row, and solve for 2/3 of 90, X’s distance.