First, here are 12 practice problems. Solutions will be given at the end of this article.
1) Two teachers, Ms. Ames and Mr. Betancourt, each had N cookies. Ms. Ames was able to give the same number of cookies to each one of her 24 students, with none left over. Mr. Betancourt also able to give the same number of cookies to each one of his 18 students, with none left over. What is the value of N?
Statement #1: N < 100
Statement #2: N > 50
2) In a certain company, 25% of the senior staff and 17% of the junior staff participate in the voluntary equity program. Let J be the number of junior employees. If there are 600 employees total, what is the value of J?
Statement #1: J > 100
Statement #2: more than 130 employees participate in the voluntary equity program
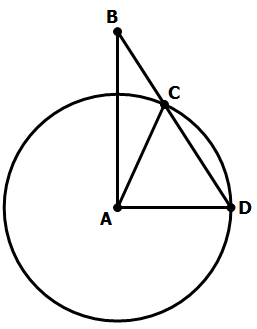
![]()
Statement #1: AB = 12
Statement #2: AD = CD
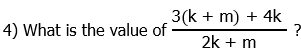
Statement #1: k + m = 9
Statement #2: k = 2m
5) Let abc denote the digits of a three-digit number. Is this number divisible by 7?
Statement #1: The two-digit number bc is divisible by 7
Statement #2: a + b + c = S, and S is divisible by 7
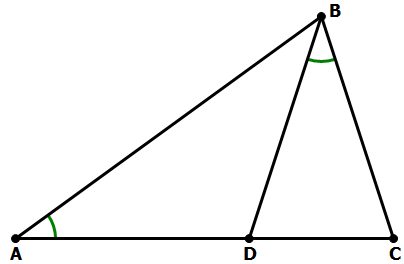
6) In the diagram above, AC = AB, and angle DAB = angle DBC. What is the measure of angle BCD?
Statement #1: angle BDC = 2*(angle DAB)
Statement #2: AD = BD
7) If N is a positive integer, does N have exactly three factors?
Statement #1: the integer N^2 has exactly five factors
Statement #2: only one factor of N is a prime number
8) Right now, a barrel of water is exactly 40% full of water. What is the volume of the barrel?
Statement #1: If the water in the barrel right now were increased by 25%, then the barrel would be exactly half full.
Statement #2: If a volume of water equal to half of what is in the barrel right now were added to the barrel, the empty space left in the barrel then would equal 75% of the volume of the water now.
9) In a set of twenty numbers, 19 of the 20 numbers are between 40 and 50. Is the median greater than the mean?
Statement #1: the standard deviation is greater than 15
Statement #2: the 20th number is greater than 500
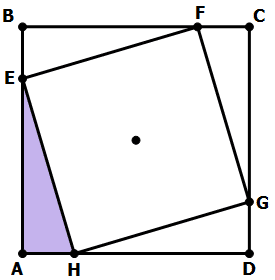
10) In the diagram above, ABCD is a square with side M, and EFGH is a square with side K. What is the value of (M + K)?
Statement #1: (M – K) = 9
Statement #2: the area of triangle AEH is 36
11) When 900 is divided by positive integer d, the remainder is r. For some integer N > 5000, when N is divided by positive integer D, the remainder is R. Is R > d?
Statement #1: r = 1
Statement #2: D = 23
12) If F is the prime factorization of N!, how many factors in F have an exponent of 1?
Statement #1: 30 ≤ N ≤ 40
Statement #2: 25 ≤ N ≤ 35
Rephrasing the question
On the GMAT, part of the challenge is deciphering what is being asked. This is particularly the case on the Data Sufficiency questions, because insofar as the prompt question is obscure, it’s hard to determine what information would be sufficient to answer this question. Part of our task on GMAT DS questions is to re-interpret the prompt question given, often discerning a much simply way to ask the same thing. Once we have a simple version, it’s that much easy to find the answer.
Unfortunately, there’s no simple rule for how to simplify such DS prompt. You have to know the fundamental mathematical definitions well, and you have to be agile in interpreting the particular combination of restraints given in a problem. Be mindful of this when you study solutions to problems: if the solutions begin by making a simplification of the prompt, probably everything after that point is relatively easy to follow, but pay attention to what the author of the solution had to notice about the problem in order to make that simplification. As I have discussed in other blogs, the primary question should not just be “what to do? what steps do I take to get to a solution?” but more “how to see? how does one reframe the problem and what it is asking?” In many cases, once we can frame the problem correctly, what to do becomes much more straightforward.
Summary
Here are some more blogs on the topic of GMAT DS.
2) GMAT Sample Data Sufficiency Practice Questions
3) GMAT Data Sufficiency: More Practice Questions
If you have any insights about rephrasing the question that you would like to share, please let us know in the comments section!

Practice problem explanations
1) This question is really about common multiples and the LCM. If Ms. Ames can give each of her 24 students k cookies, so that they all get the same and none are left over, then 24k = N. Similarly, in Mr. Betencourt’s class, 18s = N.
What are the common multiples of 18 and 24?
18 = 2*9 = 2*3*3 = 6*3
24 = 3*8 = 2*2*2*3 = 6*4
From the prime factorizations, we see that GCF = 6, so the LCM is
LCM = 6*3*4 = 72
and all other common multiples are multiples of 72: {72, 144, 216, 288, 360, …}
Statement #1: if N < 100, the only possibility is N = 72. This statement, alone and by itself, is sufficient.
Statement #2: if N > 50, then N could be 72, or 144, or 216, or etc. Many possibilities. This statement, alone and by itself, is not sufficient.
Answer = (A)
2) In this problem, it’s very important to realize: when the GMAT say “17% of the junior staff,” it doesn’t mean 16.93% or 17.02%. It means exactly, precisely, 17%. This 17% of J must be a whole number, a positive integer. The only way this can happen is if J equals either 100 or a multiple of 100. That’s a huge insight. Both J and S (the number of senior staff) must be multiples of 100 that add up to 600. In other words, there aren’t that many possibilities for the gender breakdown in this company.
Statement #1: J > 100. Well, J could be 200 or 300 or 400 or etc. Many possibilities. This statement, alone and by itself, is not sufficient.
Now, forget about statement #1!
Statement #2: Now, we have to think about the number in the equity program.
If J = 0, and S = 600, then there are 150 in the equity program. A possibility.
If J = 100 & S = 500, then 17 junior employees & 125 senior employees, which results in 142 in the equity program. A possibility.
If J = 200 & S = 400, then 34 junior employees & 100 senior employees, which results in 134 in the equity program. A possibility.
If J = 300 & S = 300, then 51 junior employees & 75 senior employees, which results in 126 in the equity program. This is not possible, and as we add more junior employees and subtract senior employees, this number will drop even lower, so there are no more possible cases.
Right now, we have many possibilities. This statement, alone and by itself, is not sufficient.
Combined: As you probably anticipated, with both statements, things are looking good. If J > 100, then the only case that allows for more than 130 in the equity program is the case with J = 200 & S = 400. We now know that J = 200, so we have definitively answered the prompt question. Combined, the statements are sufficient.
Answer = (C)
3) In order to find the area of the circle, we would need the radius, AD.
Statement #1: AB = 12. Notice that AD is the base of triangle ABD. AB is the height, now known, and we know the area. If we know the height and the area, we can find the base by A = 0.5*bh. Therefore, we can find AD, which would allow us to find the area of the circle. This statement, alone and by itself, is sufficient.
Statement #2: We know that AD = AC, because all radii of a circle are equal. If CD also equals these two, then ACD is an equilateral triangle. That means that the angle ADC = 60°, which means that triangle ABD is a 30-60-90 triangle. If AD = x is the base, then this times the square-root of 3 is the height, and we could create an equation because we know the area:
![]()
This is an equation we could solve for x, which would allow us to find the area of the circle. This statement, alone and by itself, is sufficient.
Answer = (D)
4) We can re-arrange the numerator to simplify:
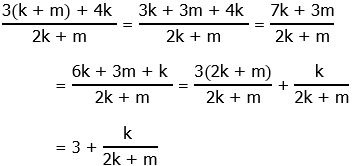
We really need to find the value of that smaller fraction, with just k in the numerator.
Statement #1: k + m = 9
This doesn’t help us. We cannot plug this in as is. If we solve for one variable, say k, and plug in, we will get an expression that doesn’t cancel. This does not lead to an answer. This statement, alone and by itself, is not sufficient.
Statement #2: k = 2m
We can plug this into the final form of the expression.
![]()
That final value we could write as a mixed numeral or change to an improper fraction, but it doesn’t matter: we have a numerical value for the expression. This statement, alone and by itself, is sufficient.
Answer = (B)
5) Statement #1, by itself, doesn’t help us. The number 49 is divisible by 7, but think about 149, which equals (100 + 49): the divisor 7 would divide evenly into 49, but it wouldn’t divide evenly in to 100, so 149 can’t possibly be divisible by 7.
Another way to think about it: 140 is a multiple of 7, so 147 must be, and 154 must be as well. The number 149 falls between the multiples of 7. (In fact, you would not need to know this for the GMAT, but 149 is a prime number.)
Of course, if the hundred’s digit is 7, then all the number of this form would be divisible by 7: 735, 742, 749, 756, etc. So, we can get either a yes or a no answer with this statement.
This statement, alone and by itself, is not sufficient.
Statement #2: a + b + c = S, and S is divisible by 7
This is reminiscent of the trick for divisibility by 3. That trick works for 3, but it doesn’t work for 7!!
Yes, we could find a number, such as 777, which is divisible by 7 and whose digits add up to 21, also divisible by 7. That number would produce a “yes” answer with this prompt.
But we also could find a number such as 223. The digits add up to 7, so this could be the number according to statement #2. Think about the multiples of 7 in that vicinity. Clearly, 21 is a multiple of 7, so 210 must also be. From there, 210, 217, 224, 231, etc. The number 223 is between the multiples of 7, so it not a multiple of 7. (In fact, you would not need to know this for the GMAT, but 223 is also a prime number.) This produces a “no” answer. Two different prompt answer possible.
This statement, alone and by itself, is not sufficient.
Combined statements:
For our “yes” representative, we can pick 777: the last two digits form 77, a number divisible by 7; the sum of the digits is 21, divisible by 7; and the number 777 is most certainly divisible by 7.
For our “no” representative, we can pick 149: the last two digits form 49, a number divisible by 7; the sum of the digits is 149, divisible by 7; and, as discussed above, the number 149 is not divisible by 7.
Even with both statements, two prompt answers are possible. Even together, the statements are not sufficient.
Answer = (E)
(This is totally beyond what you would need to know for the GMAT, but the numbers 149 and 421 and 491 and 563 are the three digit numbers that satisfy both statements but are prime!!)
6) From the prompt, we know that triangle ABC is isosceles, with AB = AC and angle ABC = angle DCB. Because angle DAB = angle DBC, and they share the angle at C, we know triangle BCD is similar to triangle ABC; therefore, triangle BCD must also be isosceles, with BC = BD and angle BDC = angle BCD. For simplicity, let’s say that
x = angle DAB = angle DBC
y = angle ABC = angle DCB = angle BDC
We know that (x + 2y) = 180°, and the prompt is asking for the value of y.
Statement #1: angle BDC = 2*(angle DAB)
In other words, y = 2x. Then
x + 2y = x + 4x = 5x = 180°
This means x = 36° and y = 72°. This statement leads directly to the numerical value sought in the prompt. This statement, alone and by itself, is sufficient.
Statement #2: AD = BD
This tell us that triangle ABD is also isosceles. This means that angle DAB = angle ABD. Think about angle ABD. That angle is the “leftover” between two angles we have already discussed:
angle ABD = (angle ABC) – (angle CBD) = y – x
Well, angle DAB = x, so if these two are equal, this means:
y – x = x
y = 2x
This turns out to be the exact same information that was given in statement #1, which we already know is full sufficient.
Answer = (D)
(BTW, more than you need to know for the GMAT, but these are Golden Triangles, because the ratio AB/BC equals the Golden Ratio! )
7) This is a question about prime numbers in disguise. Of course, any prime number has exactly two factors: 1 and itself. If we multiple two different primes, say 2 and 5, we get a number with four factors: the factors of 10 are {1, 2, 5, 10}. The only way to get a number with exactly three factors is if the number is the perfect square of a prime number. For example, 9 is the square of 3, and the factors of 9 are {1, 3, 9}; 25 is the square of 5, and the factors of 25 are {1, 5, 25}. If P is a prime number, then the factors of P squared are (a) 1, (b) P, and (c) P squared. Three factors. That’s what the question is asking. Is N the perfect square of a prime number.
Statement #1: very interesting.
If N is a prime number itself, then its square only has three factors. Squaring a prime doesn’t produce enough factors. This doesn’t meet the condition of this statement.
If N is the product of two primes, then its square has 7 factors. For example, 2*5 = 10, and 10 square is 100 which has seven factors: {1, 2, 4, 5, 10, 20, 25, 100}. Squaring a product of primes produces too many factors. This also doesn’t meet the condition of this statement.
The only way the square of N could have five factors is if N is the square of a prime number. Suppose N = 2 square, which is 4. Then N squared would be 16, which has five factors: {1, 2, 4, 8, 16}. In general, if P is a prime number, and N equals P squared, then N squared would equal P to the 4th power, which has five factors:
![]()
Therefore, N must be the square of a prime number, so we can give a clear “yes” answer to the prompt question. This statement, alone and by itself, is sufficient.
Statement #2:
This is tricky. If we know that N is the square of a prime number, then this statement would be true, but that’s backwards logic. We want to know: if this statement is true, does it allow us to conclude that N is the square of a prime number? If only factor of N is a prime number, then N could be:
(a) a prime number: the only prime factor of 7 is 7.
(b) any power of a prime number: the only prime factor of 7 to the 20th is 7
So N could be the square of a prime number, or just the prime number itself, or the cube of the prime number, or the fourth power, or etc. Any number of factors would be possible, so we have no way to answer the question. This statement, alone and by itself, is not sufficient.
Answer = (A)
8) In this problem, both statements are tautological. That is to say, each one, in a less-than-obvious way, rephrases the information in the prompt. In a way, we simply have the same information, the information already given in the prompt, recycled in three different ways. No new information is added by either statement.
From the prompt, we know that the barrel is 40% full of water right now.
Well, suppose a barrel is 40%, and we increase the water by 25%, or 1/4. That would mean adding a quarter of 40%, or 10% of the barrel to what is already in the barrel. This would increase the barrel to 50%, which is exactly what statement #1 tells us.
Go back to the 40% full barrel: the empty space is 60%. Half of that is 30%. Suppose we add 30% more: then the water would be 70% of the barrel, and the new empty space would be 30%. The new empty space, 30%, is 3/4, or 75%, of the old amount of water, 40%. This is exactly what statement #2 tells us.
Of course, the prompt by itself is never sufficient, and if neither statement adds any new information, then even altogether, we can’t deduce anything.
A totally different way to say this is: the prompt is asking for an actual quantity, the real volume of the barrel, but the prompt & statements give us nothing but ratio information (including percents & fractions). We need a real measurement to get a real measurement, and we never get one in this problem.
Nothing is sufficient.
Answer = (E)
9) For a symmetrical distribution, the mean = median, and if the median is close to symmetry, the mean and the median are close in value. When the distribution of numbers is radical asymmetrical, with one outlier or several outliers on only one side of the distribution, then the mean is pulled in the direction of the outliers. The median, resistant to outliers, stays in the middle of the majority of numbers, but the mean is sensitive to outliers, gets pulled in their direction. High outliers pull the mean up, and low outliers pull the mean down.
Statement #1: the standard deviation is greater than 15
This tells us that there’s large variation, suggesting that the 20th number is far away from the other 19, but far away in which direction? Much higher or much lower than the rest of the numbers? We don’t know. A high outlier would pull the mean up, and a low outlier would pull the mean down. Here, we know we have an outlier, but we don’t know its directions, so we don’t know in which direction the mean is affected. We cannot answer the question. This statement, alone and by itself, is not sufficient.
Statement #2: the 20th number is greater than 500
Now, we know that the outlier is a high outlier, much bigger than the other numbers in the set. A high outlier pulls the mean up, away from the median, so the mean is higher than the median. We can give a definitive “yes” answer to the prompt question. This statement, alone and by itself, is sufficient.
Answer = (B)
10) In the diagram, we literally have two squares, M squared and K squared. The four right triangle are what we get if we subtract one square from the other: they are literally the difference of two squares, so we can use the Difference of Two Squares formula:
![]()
We could find (M + K) if we knew (M – K) and the difference of the squares.
Statement #1: this gives us (M – K), but we don’t know the difference of the two squares. This statement, alone and by itself, is not sufficient.
Statement #2: this gives us the area of one triangle, and if we multiply by 4, we have the difference of the two squares. But, now we don’t know (M – K), so we can solve. This statement, alone and by itself, is not sufficient.
Combined statements. With the two statements, we know both (M – K) and the difference of the squares, so we can solve for (M + K). Together, the statements are sufficient.
Answer = (C)
11) This is a tricky one about remainders.
Statement #1: If r = 1, then we divide 900 by d, and the remainder is 1. This means that d is a factor of 899. That’s interesting, but at the moment, we know zilch about R, which could be anything. This statement, alone and by itself, is not sufficient.
Statement #2: If D = 23, then when we divide by 23, the remainder has to be smaller than the divisor. We know R < 23. But, now, the only thing we know about d is that it’s not a factor of 900: d could be 7 or 97. We have no idea of its size, so we can’t compare it to R. This statement, alone and by itself, is not sufficient.
Combined:
From the second statement, we know R < 23. From the first, we know d must be a factor of 899. What are the factors of 899? For this we will use an advanced factoring technique. Notice that 899 = 900 – 1. This means, we can express 899 as the Difference of Two Squares, because 900 is 30 squared. We can use that algebraic pattern to factors numbers.
![]()
So, it turns out that 899 is the product of two prime numbers, 29 and 31. This means that 899 has four factors: {1, 29, 31, and 899}. Those are the candidate values for d. Obviously, d cannot equal 1, because when we divide any integer by 1, we never get a remainder of any sort: 1 goes evenly into every integer. That means, d could be 29 or 31 or 899. Well, if R < 23, this means that R must be less than d. We can give a definitive “yes” answer to the prompt question. Combined, the statements are sufficient.
Answer = (C)
12) This is a tricky one.
Let’s think about, say, 40! This number, 40!, is the product of all the integers from one to 40. Let’s think about its prime factorization. It would have at least one factor of 2 for every even number from 2 to 40, and a second factor for every multiple of 4, and a third factor for every multiple of 8, etc.; a lot of factors of two. Think about the factors, say, of 7: there are five multiples of 7 from 7 to 35, so in the prime factorization of 40!, the factor 7 would have an exponent of 5. Which factors would have exponents of 1? Well, the prime numbers that are less than N, but have no other multiples less than N. For example, in 40!, the factor 37 would have an exponent of 1 since it appears once and no other multiple of it is less than 40.
Statement #1: 32 ≤ N ≤ 40
As we move through different N’s in this region, we cross the prime number 37, which will have an exponent of 1 if it appears. Some N’s include this prime number and some don’t, so the number of factors with an exponent of 1 is different for different values of N. This statement, alone and by itself, is not sufficient.
Statement #2: 27 ≤ N ≤ 35
As we move through different N’s in this region, we cross two prime numbers, 29 and 31, each of which will have an exponent of 1 if it appears. Some N’s include neither, some include 29 and not 31, and some include both, so the number of factors with an exponent of 1 is different for different values of N. This statement, alone and by itself, is not sufficient.
Combined: 32 ≤ N ≤ 35
Now, there are no prime values in the range specified. But, here’s a tricky thing. If N = 32 or 33, then either 32! or 33! contains exactly one factor of the prime numbers {17, 23, 29, 31}: four prime factors with an exponent of one. BUT, if N = 34 or 35, there are now two factors of 17 (one from 17 and one from 34), either 34! or 35! contains exactly one factor of the prime numbers {23, 29, 31}: three prime factors with an exponent of one. Even in this narrow range, different choices lead to different answers for the prompt question. Even together, the statements are not sufficient.
Answer = (E)





Leave a Reply