Diagrams are great! Like all types of scratch-work, diagrams can forestall cognitive fatigue because working a problem out on paper is much less demanding than doing all the work in your head. Diagrams can also help you to visualize relationships, and can make problems more concrete.
Generally though, we use diagrams to generate equations, which we still have to solve. So good scratch-work doesn’t substitute for other mathematical ability.
Today we’ll use speed problems as examples, since they’re the most common sort of GMAT rate problem, but we’ll talk about work-rate and other problems in a couple of days.
Let’s jump into an example!
This is a pretty stock example:
- It involves exactly two travelers.
- Those travelers are moving in opposite directions. In this case they’re moving apart, but in other problems they’ll be moving toward one another.
- Those travelers are moving simultaneously, at least for the portion of their travels that concern us.
Train X and train Y pass one another traveling in opposite directions. Forty minutes later they are 100 miles apart. If train X’s constant speed is 30 miles per hour greater than train Y’s, how far does train X travel during that time?
A. 28
B. 40
C. 60
D. 72
E. 80
The diagram we’ll use for this problem is a RTD Table. It consists simply of three columns (for rate, time, and distance) and some number of rows. For this problem we’ll use three rows, one for each of the trains and one for their combined rate:
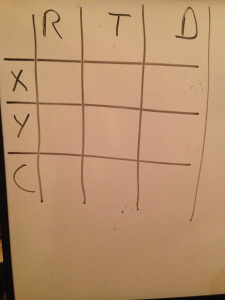
If you like, you can include multiplication and equality signs, to remind yourself how the values in each row are related to one another: RT=D. I’ve included those signs below in red, but in subsequent illustrations of the table I’m going to leave them out. I will include one more thing though. Circle or otherwise indicate the cell for which we’re solving. In this case, that’s X’s distance.
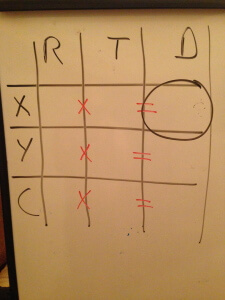
Begin by writing in whatever information is given to you. In this case that would include the combined distance traveled by the two trains, and the time traveled.
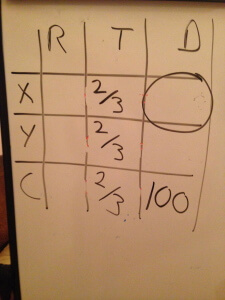
A few notes: (1) We didn’t include a distance for either train X or train Y, because we’re not given those. (2) For every story about simultaneous travel, the time value will be the same all the way down the column. (3) In this case that time value is 2/3 of an hour. Yes, it was given to us as 40 minutes, but since the speed is given to us in miles per hour, we need to change something to keep the units consistent. It’s often easier to change from a few large units (like hours) to many small units (like minutes) but in this case I chose to stick with hours. (4) If you’re consistent in your units, and if the units in the table are the same as in the answers, units don’t really matter any more. In math class, you’d probably represent the units, but I’m not going to bother.
Also capture the rate for each of the trains, using as few variables as possible. In this case, that might mean calling train X’s rate simply r and calling train Y’s rate r-30, since we’re given that train X’s constant speed is 30 miles per hour greater than train Y’s. (You could also have called train Y’s rate r and train X’s rate r+30.)
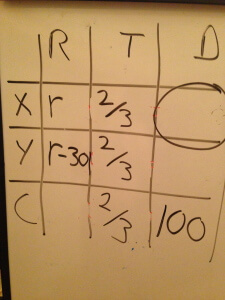
Next add the rates of the two trains to get their combined rate. Every time that you have a story about two travelers moving in opposite directions (whether toward each other or away from each other) and moving simultaneously (starting and stopping at the same time, or both moving for the entire portion of the journey that you’re concerned with) add the rates.
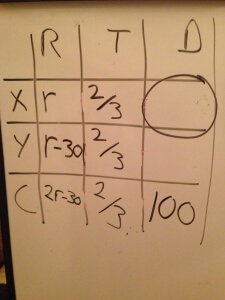
We now have a complete equation in the bottom row. Since RT=D, we can see that (2r-30)(2/3)=100. Solve for r:
(2r-30)(2/3)=100
(4r/3)-20=100
4r/3=120
4r=360
r=90
Notice that the diagram merely generated this equation for us; it didn’t solve the equation. Of course, our ultimate goal is not to solve for r but to solve for the distance traveled by X. Substitute 90 for r and complete the row for X.
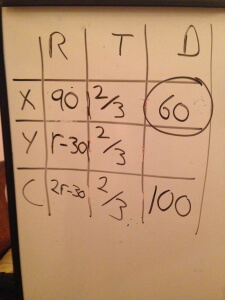
Couldn’t we do that without the table?
Yep. We could have simply noted that for any simultaneous travel problem (combined rate)(time)=(combined distance). We’re given the time (2/3) and combined distance (100 miles). If we can manage to represent the combined rates (2r-30) we should be able to solve for r. If we can also characterize what we’re solving for (2/3 of r) then we can answer the question.
Some people can do all of that without the table.
On the other hand, some people who can do all of that without the table in practice find that they need help organizing and translating information once they’re well into the test. So it’s worthwhile learning to use the table.
Another reason to learn to use the table is that some rate problems are a lot more subtle than this one. We’ll look at such problems in a couple of days.






Leave a Reply