
Learn to master an area the GMAT loves to test.
The Cartesian Plane (a.k.a. the x-y plane) is a favorite GMAT topic, especially on GMAT Data Sufficiency. It’s a simple topic, but with just enough subtlety that the testmakers can spin endless questions from it.
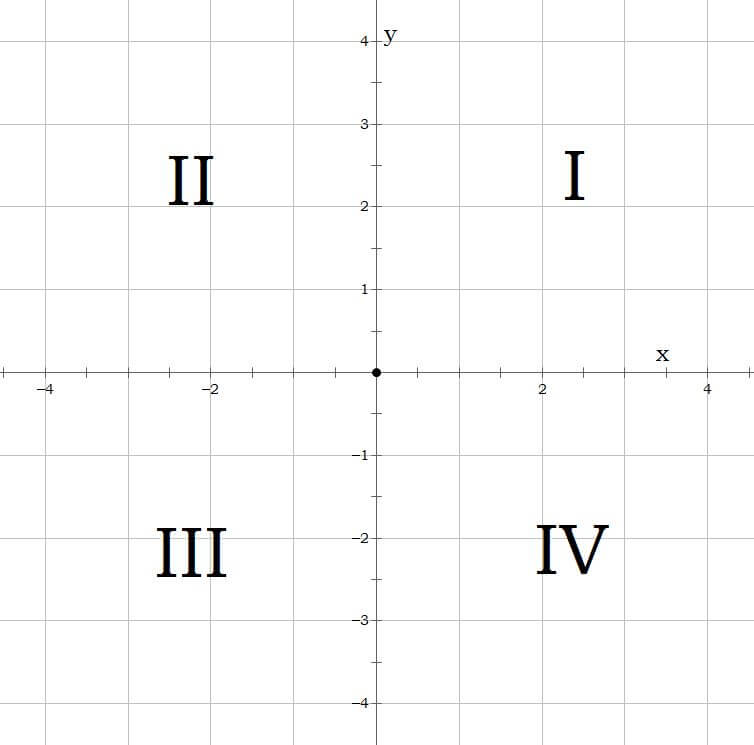
Quadrants
The quadrants begin with I, where both x and y are positive, and rotate counterclockwise from there. Notice
Mixing in arithmetic operations
OK, still relatively simple, but now what happens when you multiply or divide the x- and y-coordinates? Both (positive)*(positive) and (negative)*(negative) are positive, but if one factor is positive and one is negative, the product is negative. Similarly, (positive)/(positive) and (negative)/(negative) are positive, but if dividend is positive & divisor negative, or vice versa, the quotient is negative. Thus:
Already, that’s rich fodder for GMAT Data Sufficiency. Now, what happens when we add the x- and y-coordinates? (positive) + (positive) = (positive), and (negative) + (negative) = (negative), but (positive) + (negative) — hmmm — the sign of the sum depends on which has a larger absolute value. Thus:
In QI, x + y > 0
In QII, the sign of x + y is unclear (i.e. it depends on the values of x & y)
In QIII, x + y < 0
In QIV, the sign of x + y is unclear (i.e. it depends on the values of x & y)
Even worse: subtraction! We know a (positive) – (negative) must be positive, and a (negative) – (positive) must be negative, but if we have either a (positive) – (positive) or (negative) – (negative), then the sign of the difference depends on which has a larger absolute value. Thus:
In QI, the signs of (y – x) and (x – y) are unclear (i.e. it depends on the values of x & y)
In QII, y – x > 0 and x – y < 0
In QIII, the signs of (y – x) and (x – y) are unclear (i.e. it depends on the values of x & y)
In QIV, y – x < 0 and x – y > 0
Now, you probably have some appreciation of how many potential Data Sufficiency Questions the GMAT could concoct simply on the quadrants and the signs of x & y coordinates. A simple topic, but one worth thinking through thoroughly so you are ready on test day.
Practice questions:
1) Is the point (x, y) in the fourth quadrant?
(1) xy > 0
(2) y > 0
2) http://gmat.magoosh.com/questions/1031
The question at that link will be followed by a video explaining the solution.
Practice question explanations
1) This DS question is a yes/no question. We don’t actually need to determine the quadrant of (x, y), only whether it’s in QIV.
Statement #1: xy > 0
This inequality means that the (x,y) is either in QI or QIII, as we saw above. We don’t know which, but in either case, we can definitively say: no, it’s not in QIV. Because the statement allows us to arrive at a definitive answer — and it doesn’t matter one peep whether it’s a yes or no answer, as long as it’s definitive — the statement is sufficient. We got a definitive no answer to the question, so Statement #1 is sufficient.
Statement #2: y > 0
This inequality means that the point (x,y) is north of the x-axis, in either QI or QII. We don’t know which, but in either case, we can definitively say: no, it’s not in QIV. Again, definitive answer to the question, so Statement #2 is sufficient.
Both statements sufficient: answer = D.
The solution & explanation to question #2 are available at the link above.


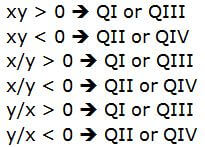





Leave a Reply