Learn the geometry properties of this important category of shapes and be ready for GMAT Quant questions about them!
Definition
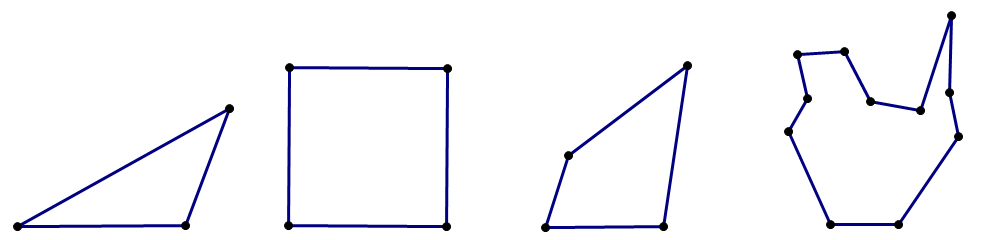
A polygon is a closed 2D shape with all straight sides. Every side has to be a line segment. The following are all polygons:
There must be at least three sides, but there is no upper limit to the total number of sides, as long as all the sides are straight. The circle is not a polygon, nor is anything with a curved side. Everything in this post will true only for polygons.
A polygon with three sides is a called a triangle. A polygon with four sides is called a quadrilateral; special cases of quadrilaterals include shapes like trapezoids, rectangle, rhombuses, and squares. A polygon with five sides is a called a pentagon. A polygon with six sides is a called a hexagon. A polygon with eight sides is a called an octagon. I mention these names for the purpose of discussing these shapes in this article, but in all likelihood, you will not need to know those last two terms for the GMAT. There are different names for each number of sides above 6, but you certainly don’t need to know all those names for the GMAT.
Angles in polygons
Here are some facts true for the general run-of-the-mill polygons out there. No matter how bizarre and asymmetrical a polygon is, it must obey these rules.
1. In any triangle, the sum of the three angles is 180°.
2. In any quadrilateral, the sum of the four angles is 360°.
Both of these facts appeared first in the writings of Euclid (fl. c. 300 BCE), the Father of Geometry. Most folks probably dimly remember fact #1, but fact #2 may be a little less familiar. Why is fact #2 true? You can divide any quadrilateral into two triangles, and the angles in each triangle add up to 180°, so all the angles in the quadrilateral must add up to twice that, 360°. It turns out you can extend that pattern to pentagons and higher polygons: in fact, the formula is:
The sum of the angles in an n-sided polygon = (n – 2)*180°
Regular polygons
This is one of the more ironic terms in all of mathematics. In everyday life, the word “regular” means ordinary, commonplace, not at all special. In geometry, the word “regular” means the exact opposite: the most elite of all shapes — elite, because of their high degree of symmetry.
In order to be regular, a polygon must satisfy both of the following conditions
1. the polygon must be equilateral (i.e. all sides have the same length)
2. the polygon must be equiangular (i.e. all angles have the same measure)
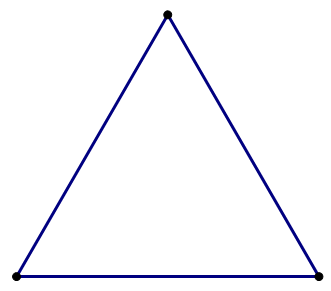
Interestingly, for a triangle, those two conditions are not separable: every equilateral triangle must be equiangular, and every equiangular triangle must be equilateral. In an equilateral triangle, a.k.a. a regular triangle, all three sides are equal, and each angle equals 60°.
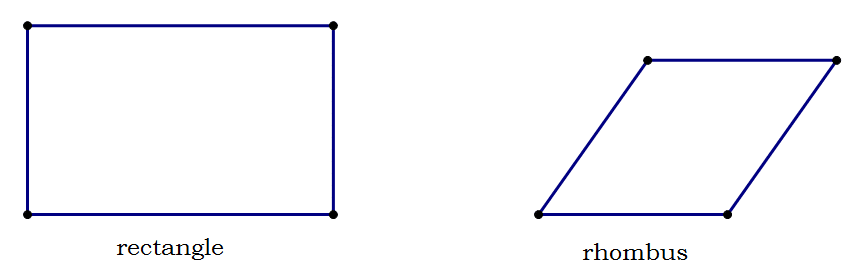
With quadrilaterals and all higher polygon, the conditions of equilateral and equiangular are separable. For example, a rectangle is a quadrilateral which is equiangular (all four angles equal 90°), but not necessarily equilateral; and a rhombus is a quadrilateral that is, by definition, equilateral, but may or may not be equiangular.
Incidentally, the rectangle on the left is the Golden Rectangle. As you may suspect, the elite quadrilateral, the regular quadrilateral with the highest degree of symmetry, is the square.
Because the square is the most elite quadrilateral, it is a very special case — yet, because it is such a familiar shape, test takers frequently make the gullible mistake of assuming any odd quadrilateral is a square. That would be as if I told you no more than that my next door neighbor’s first name began with a vowel, and immediately you jumped to the conclusion that my next door neighbor absolutely must be Pulitzer Prize winning author Alice Walker. This is the gullible mistake of getting only very general, vague information and from that drawing a highly specific conclusion. See this post for more on that mistake concerning the square.
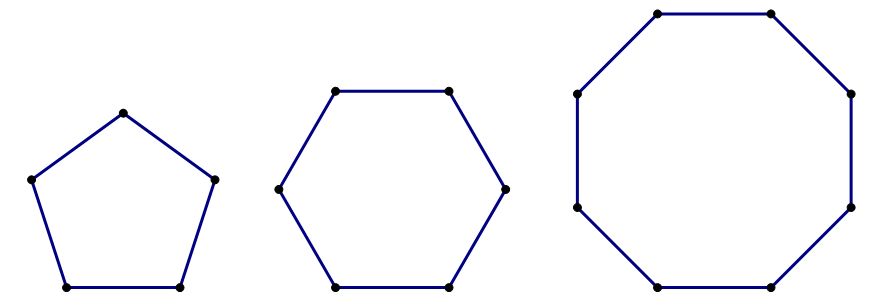
Below are three more regular shapes: from left to right, the regular pentagon (each angle = 108°), the regular hexagon (each angle = 120°), and the regular octagon (each angle = 135°).
The hexagon is the shape of most standard bolts. The octagon is the shape of stop signs in most of the world, but neither in Japan nor in Zimbabwe.
A rare advanced GMAT Quant question could expect you to know the angles in one of these last three shapes. Each one has numerous wondrous geometric properties, but those are well beyond what you need to know for the GMAT. Below are some practice questions.
Practice problems
1) In the figure above, in irregular quadrilateral ABCD, ∠A = 60°, ∠D is twice ∠C, and ∠B is 40° more than ∠C. Find the measure of ∠B
A. 65°
B. 85°
C. 105°
D. 120°
E. 135°
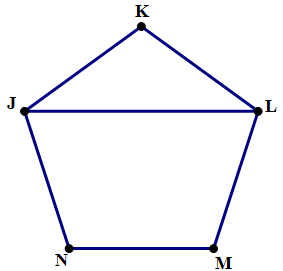
2) In the figure above, JKLMN is a regular pentagon. Find the measure of ∠JLK.
A. 24°
B. 36°
C. 48°
D. 60°
E. 72°
Practice problem explanations
1) The sum of the four angles in a quadrilateral is 360°. We know ∠A = 60°. Let ∠C = x —- then ∠D = 2x and ∠B = x + 40°.
∠A + ∠B + ∠C + ∠D = 360°
60° + (x + 40°) + x + 2x = 360°
4x + 100° = 360°
4x = 260°
2x = 130°
x = 65° —- that’s the measure of ∠C, and ∠B is 40° more than this.
∠B = 65° + 40° = 105° —- Answer = C
2) This would be a particularly challenging high level GMAT Quant problem. Here, you are expected to remember that each angle inside a regular pentagon equals 108° —- only the most difficult 700-level questions would expect you to recall something like that.
Given that ∠K =108°, we also know that triangle JKL is isosceles — since the pentagon is equilateral, it must be true that JK = KL, and that in turn would mean ∠J = ∠L. Let those angles equal x. Then, in triangle JKL,
∠J + ∠K + ∠L = 180°
x + 108° + x = 180°
2x + 108° = 180°
2x = 72°
x = 36° —- ∠J = ∠L = 36°, so Answer = B
BTW, in that problem, triangle JKL is a Golden Triangle, because the ratio
The Golden Ratio was revered as sacred in many ancient cultures, and it plays an integral role in the images of artists such as Leonard da Vinci, Georges Seurat, and Piet Mondrian. It’s not especially important to know for the GMAT, but a fascinating rabbit hole to explore extensively when at leisure.




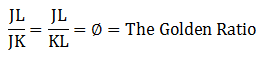




Leave a Reply