In the previous post in this series, we looked at arc measure and arc length. Now it’s time to look at circles and straight lines.
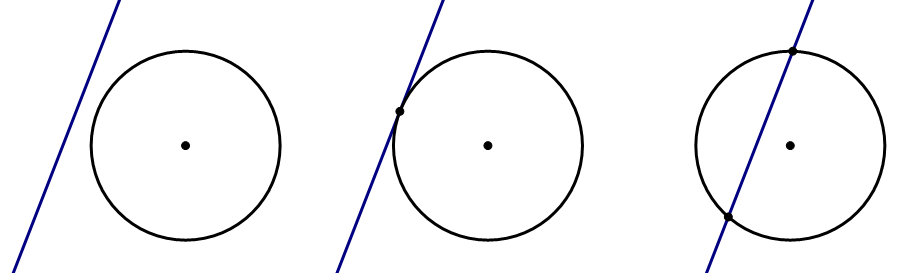
What happens when a straight line comes near a circle? In how many ways can these two objects intersect? It turns out, there are three possibilities — see below: no intersection, one intersection, or two intersections.
In the first case, no intersection, nothing interesting happens, so there’s no special name for that. In the second case, the line just “touches” circle at one point, so it’s called a tangent line; the word tangent, a “touching” line, shares an etymological root with the word tangible, meaning “touchable.” In the third case, the line cuts through the circle, so it’s called a secant line; the word secant means “cutting”, and shares an etymological root with other “cutting” words, such as: dissection, intersection, bisect, sector, section, etc.
There’s nothing particular special about secant lines. The part of the secant line between the two intersection points is, of course, a chord. Remember, the diameter is a chord, the longest possible chord, so the chord on a secant line would be diameter if the secant line happened to pass through the center of the circle. In Geometry, there are sorts of complicated theorems about the angle between two secant lines both intersecting the same circle, but that gets into territory well beyond the GMAT Quant.
Tangent lines
Tangent lines are more interesting, and there’s a very important fact about tangent line that the GMAT will expect you to know. Consider a line tangent to a circle at point A, and a radius also drawn to point A.
As you might suspect: a tangent line is always perpendicular to a radius at the same point. In other words, it absolutely must be true that ∠OAB is exactly a 90° angle. That’s a fact you need to know for the GMAT Quant section.
Below are a couple practice questions. In the fourth post in this circle series, I will talk about circles and polygons. In fact, here’s the whole series.
1) Introduction to Circles on the GMAT
2) GMAT Geometry: Circles and Angles
3) Circle and Line diagrams on the GMAT
4) Inscribed and Circumscribed Circles and Polygons on the GMAT
5) Slicing up GMAT Circles: Arclengths, Sectors, and Pi
Practice problems
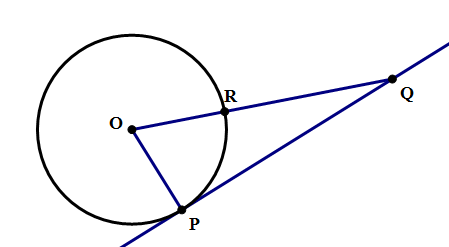
1) In the diagram above, line PQ is tangent to the circle, and the measure of arc PR is 70°. What is the measure of ∠PQR?
A. 15°
B. 20°
C. 25°
D. 30°
E. 35°
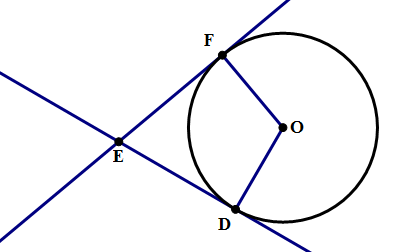
2) In the diagram above, lines EF and DE are each tangent to the circle. If ∠FOD = 110°, what is the measure of ∠DEF?
A. 40°
B. 50°
C. 60°
D. 70°
E. 80°
Practice problem explanations
1) First of all, since the measure of arc PR is 70°, we know the angle at the center, ∠POR, must also be 70°. We know that ∠OPQ = 90°, because PQ is a tangent line. Now look at triangle OPQ. We know that the three angles in that triangle must add up to 180°.
∠POR + ∠ OPQ + ∠ PQR = 180°
70° + 90° + ∠ PQR = 180°
160° + ∠ PQR = 180°
∠ PQR = 180° – 160° = 20°. Answer = B
2) We are told that ∠FOD = 110°, and we know that ∠EFO = ∠EDO = 90°, because those two lines are tangent lines. Now look at quadrilateral ODEF. We know that the sum of the four angles of any quadrilateral has to equal 360°.
∠EFO + ∠EDO + ∠FOD + ∠ DEF = 360°
90° + 90° + 110° + ∠ DEF = 360°
290° + ∠ DEF = 360°
∠ DEF = 360° – 290° = 70°. Answer = D






Leave a Reply