Some questions to start: Can a square root be negative? Yes, there is such a thing as a negative square root. How would you deal with negative roots on the GRE? This question is actually fairly complicated, because it depends on how the GRE words the question. Let’s start with some GRE math practice problems before I explain.

Negative square root practice problems
First of all, consider these two similar, but not identical, Quantitative Comparison questions. These are a bit easier than you would see on the GRE, but they illustrate an important distinction about possible negative square roots.
1)

2)
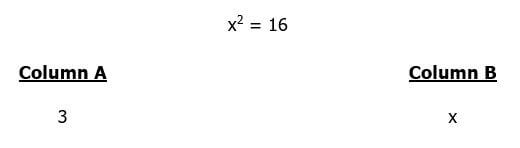
All I will say right now is: despite apparent similarities, those two questions about whether roots are positive or negative, have two completely different answers. The distinction between them is the subject of this article.
Explanations to these practice problems will appear at the end of this blog article. Jump ahead by clicking here.
Do I include the negative roots?
Often, students are confused about this question. For example, in the questions above, we know +4 is a square root of 16, but can’t -4 be one as well? Or can it? Can a square root be negative? Do we include the negative square root as part of Column B or not? Does it matter how the question is framed? All of these questions about possible negative square roots are resolved by understanding the following two cases.
Case I: the symbol appears
In case one, the test-maker, in writing the question, uses this symbol. This symbol appears printed on the page in the question itself.

What is this symbol? Well, the most folks call this simply a “square-root” symbol, but the proper name is the “principal square root” symbol. Here, “principal” (in the sense of “main” or “most important”) means: you take one and only one root, the most important, or principal, one — the positive root only. That is the deep meaning of this symbol.
Thus, in all cases in which this symbol appears as part of the question itself, you NEVER consider the negative square root, and ONLY take the positive square root.
Case II: the symbol doesn’t appear
In this case, that special symbol does not appear as part of the problem. What does appear is, for instance, a variable squared, or some other combination of algebra that leads to a variable squared, and you yourself, in your process of solving the problem, have to take the square root of something in order to solve it. The act of “square rooting” is not initiated by the test maker in the act of writing the question; rather, it is you who initiated the square-rooting.
In this case, 100% of the time, you ALWAYS have to consider both the positive and negative square roots.
Summary: Can a square root be negative?
Can a square root be negative? Well, the answer is: it depends on what was printed in the problem. The principal square root symbol never has a negative output, so if the test maker printed that symbol, it’s restrictions have to be respected: all square roots then are positive. On the other hand, if the problem contains a variable squared, or some other algebra that leads to a variable squared, and you yourself take a square root as part of the act of solving, then you always have to consider all possible solutions, both the positive square roots and the negative square roots.
If you master that distinction, you will always understand when to consider both positive and negative roots vs. when to consider only the positive root. You may want to go back to those two QCs at the beginning and think them through again before reading the solutions below.
Additional resources
If you’re having trouble with Quantitative Comparison questions on the GRE, I would recommend taking a look at some of these additional resources. They may help clear up some of the concepts that you’re struggling with, and can provide some extra practice.
Quantitative Comparison Tips
- QC Tip #1: Dealing with Variables
- QC Tip #2: Striving for Equality
- QC Tip #3: Logic Over Algebra
- QC Tip #4: Comparing in Parts
- QC Tip #5: Estimation With a Twist
Quantitative Comparison Strategies
- QC: The Devil Is in the Details
- QC: “The relationship cannot be determined from the information given” Answer Choice
- QC and Manipulation
- GRE Math: Solving Quantitative Comparisons
Quantitative Comparison Practice
GRE Math Help
Practice problem solutions
1) Here, the principal square root symbol appears as part of the problem itself. We are in Case I. Of course, that symbol means: take the positive square root only. So Column B can only equal +4. Of course, that’s always bigger than 3. Answer = (B).
2) Here, there’s no square root symbol printed as part of the problem itself. We are in Case II. For any square roots we take as part of our solution, we are liable to account for both the positive and negative roots.
Sure enough, the very first thing we encounter in the prompt is a variable squared, and when we solve for x, we have to account for both roots: x = ±4. The variable x could equal well have either one of those values.
Now, when we proceed to the QC, we see that the different values of x would give different answers. If x = +4, then column B is greater, but if x = -4, then column A is greater. Different values lead to different conclusions, and this situation means we don’t have enough information to establish a definitive relationship. Answer = (D)
Special Note:
To find out where roots sit in the “big picture” of GRE Quant, and what other Quant concepts you should study, check out our post entitled:
What Kind of Math is on the GRE? Breakdown of Quant Concepts by Frequency
Editor’s Note: This post was originally published in September, 2012, and has been updated for freshness, accuracy, and comprehensiveness.






Leave a Reply