
To begin, here are four reasonably challenging practice problems.
1) S is a set of n consecutive positive integers. Is the mean of the set a positive integer?
Statement #1: the range of S is an even integer
Statement #2: the median of S is a positive integer
2) If N = 255 is the lowest of a set of 23 consecutive multiples of 15, what is the range of this set?
-
- (A) 315
-
- (B) 330
-
- (C) 345
-
- (D) 360
- (E) 375
![]()
I. 4
II. 6
III. 18
-
- (A) I only
-
- (B) II only
-
- (C) I and II only
-
- (D) II and III only
- (E) I, II, and III
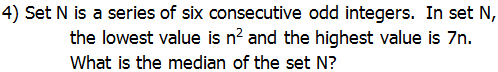
-
- (A) 5
-
- (B) 10
-
- (C) 25
-
- (D) 30
- (E) 35
Explanations for these will come at the end of the article.
Consecutive Integers
The word “consecutive” means “in a row; one after the other.” A set of three consecutive integers might mean {3, 4, 5} or {137, 138, 139} or {–25, –24, –23}. As long as the integers are in a row, it doesn’t matter whether they are big or small, positive or negative. In fact, the set {–1, 0, +1} contains one positive number and one negative number (of course, zero is neither positive nor negative).
Properties of Consecutive Integers
a) Any set of n consecutive integers will contain exactly one number divisible by n. For example, any three integers in row must contain a multiple of 3; any 17 integers will contain one multiple of 17, etc. Now, you may look at the set {–1, 0, +1}, a set of three consecutive integers, and wonder: where is the multiple of 3? This is tricky. As it turns out, zero is a multiple of every integer, because (any integer) times zero equals zero.
b) In a set of three consecutive integers, we could have two evens and one odd, or two odds and one even, depending upon where we started. In a set of four consecutive integers, we would have to have two evens and two odds. More generally, if we have an odd number of consecutive integers, we could have more evens or more odds, depending on the starting value, but if we have an even number of consecutive integers, the evens and odds have to be evenly split.
c) If n is an odd number, then the sum of n consecutive integers is divisible by n. For example: for any three integers in a row, the sum is divisible by 3; for any 7 integers in a row, the sum is divisible by 7, etc.
Algebraic Representations
Anyone can recognize that {6, 7, 8, 9, 10, 11} is a set of consecutive integers. When you are given plain old numbers, it’s easy to see whether they are consecutive integers. That’s too easy. The GMAT will not ask about that. Instead, the GMAT will give you algebraic representations of consecutive integers.
The following are examples of algebraic representations of consecutive integers:
{n, n + 1, n + 2, n + 3, n + 4, n + 5}
{n – 2, n – 1, n, n + 1}
{n + 12, n + 13, n + 14}
For all of those, if n equals any integer, then the set will be a set of consecutive integers. For simplicity, let’s pick n = 10. The first set becomes the set of integers from 10 to 15; the second, from 8 to 11; and the third, from 22 to 24. Even without knowing the value of n, we can apply the properties of consecutive integers to the set: for example, the second is a set of four consecutive integers, so it must have two evens and two odds; the third is a set of three consecutive integers, so the sum of those three numbers must be divisible by three.
Summary
If you had some insights reading this article, you may want to give the problems above a second look before reading the solutions below. Here’s another practice question from inside Magoosh:
5) http://gmat.magoosh.com/questions/943
If you have questions about anything unclear in this post, please let us know in the comments section.
Practice problem explanations
1) First of all, for a set of consecutive integers, or for any set of evenly spaced numbers, the mean and the median are equal. If there’s an odd number of members of the list, then the median is the middle number. If there’s an even number of members of the list, then the median is the average of the two middle numbers. For example, the median of {1, 2, 3, 4, 5} is 3, a positive integer and member of the set. For consecutive integers, an even number of members would mean that the mean or median is the average of the two middle integers. For example, the median of {1,2, 3, 4} is the average of 2 and 3, that is, 2.5, not an integer. The only way the mean or median can be an integer is if the set of consecutive integers has an odd number of members.
Statement #1: If there are an even number of consecutive integers, then the evens and odds are balanced in the set, and the first and last number must be opposite: one must be even and the other must be odd. Thus, the range, the difference of (max) – (min) would be either (even) – (odd) or (odd) – (even), in either case, an odd number. If the range is odd, the number of consecutive integers is even.
If there are an odd number of consecutive integers, then the first and last numbers are either both even or both odd. The range would be either (even) – (even) or (odd) – (odd), in either case, an even number. If the range is even, the number of consecutive integers is odd. That must be the case here. As we have seen above, this means the mean or median is a positive integer. This statement, alone and by itself, is sufficient.
Statement #2: As we discussed above, the mean = the median. If the latter is a positive integer, so is the former. This statement, alone and by itself, is sufficient.
Both statement are separately sufficient. Answer = (D)
2) When we have a set of consecutive integers or consecutive multiples of the number, the range depends only on the size of the set, how many members, not where on the number line the set starts or ends. For example, any seven consecutive integers will have a range of 6, whether it’s 1 through 7 or 51 through 57. Thus, we can ignore the starting number, 255, which is just there to confuse us. We can pick any more convenient starting value.
Let’s start at a1 = 15 = 15*1. Then a2 = 15*2 = 30, and a3 = 15*3 = 45. Continuing in this pattern, the last number would be a23 = 15*23. Don’t multiply that yet. The range would be highest minus the lowest:
range = (a23) – (a1) = 15*23 – 15*1 = 15*(23 – 1) = 15*22
Now, use the doubling & halving trick. Half of 22 is 11, and twice 15 is 30, so
15*22 = 11*30 = 330
Answer = (B)
3) This is a tricky one. If you start plugging in values for n, you are sunk. The numbers are gigantic and unwieldy. This one begins with some clever factoring. Clearly, in the first factor, we can factor out a factor of n:
In the second one, we can us the Difference of Two Squares:
Now, put all that together, and rearrange the order:
Written in that order, we see this is a product of four consecutive integers. We absolutely know that two of the numbers are even and two are odd. If there are two even numbers, each one has a factor of two, so the product would have a factor of 2*2 = 4. The product must be divisible by 4. We know I must be true.
Any three consecutive integers contains one multiple of 3, so four consecutive integers would contain at least one. We have a multiple of 3, which has 3 as a factor, and at least one even number, which has 2 as a factor. They may be the same number or may not be: that doesn’t matter. As long as the entire product contains at least one factor of 3 and at least one factor of 2, then the product must be divisible by 6. We know II must be true.
To be divisible by 18=2*3*3, we need one factor of 2 and two factors of 3. We definitely have more than one factor of 2. The problem is: how many factors of three do we have? In a set of four consecutive integers, we could have two factors of three, as in {12, 13, 14, 15} or {6, 7, 8, 9}. BUT, we could also have a set of four consecutive integers with only one factor of three, as in {4, 5, 6, 7}. Thus, we could have two factors of three, and the product could be divisible by 18, but we are not sure. We cannot say that this must be true. Therefore, III cannot be among the answer.
Only I and II work. Answer = (C)
4) We know that odd integers are spaced two apart: if we have one odd integer, we can add 2 to get the next one. Starting from the given expression for the first member of the set, we can say:
This highest member, we can set equal to 7n
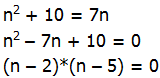
n = 2 or n = 5. Well, if n equals 2, then the first member would be 4, not an odd integer. That value doesn’t work with the problem. Therefore, we know n = 5. This means that first member is 25, and the whole set is {25, 27, 29, 31, 33, 35}. The median of this set is the average of the two middle numbers, 29 and 31; median = 30.
Answer = (D).






Leave a Reply