
Here are eight practice problems involving circles. The difficulty of these problems ranges from medium to very challenging.
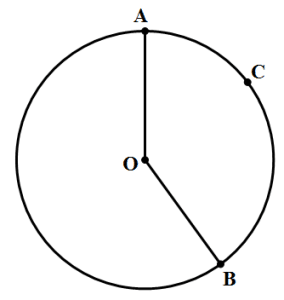
1) In the diagram above, O is the center of the circle and angle AOB = 144º. What is the area of the circle?
Statement #1: The area of sector AOB is 40% of the area of the circle
Statement #2: Arc ACB has a length of  .
.
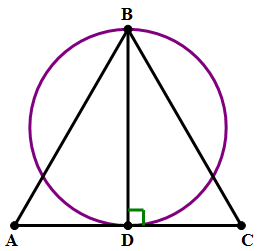
2) In the diagram above, ABC is an equilateral triangle. D is the midpoint of AC. BD is a diameter of the circle. If AD = 4, what is the area of the circle?

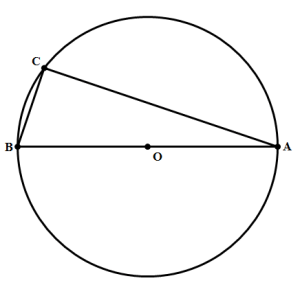
3) In the diagram above, O is the center of the circle. What is the length of chord AC?
Statement #1: chord BC = 14
Statement #2: the circle has an area of 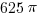
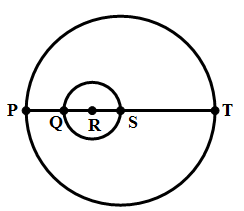
4) Points P, Q, R, S, and T all lie on the same line. The larger circle has center S and passes through P and T. The smaller circle has center R and passes through Q and S. What is the ratio of the area of the larger circle to the area of the smaller circle?
Statement #1: ST:PQ = 5/2
Statement #2: RT:PR = 13/7
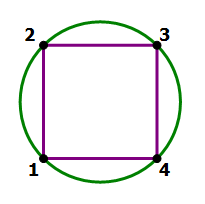
5) A square and a circle intersect at more than one point. Does the square have more area than the circle?
Statement #1: there are exactly four intersection points
Statement #2: at least two of the intersection points are on vertices of the square
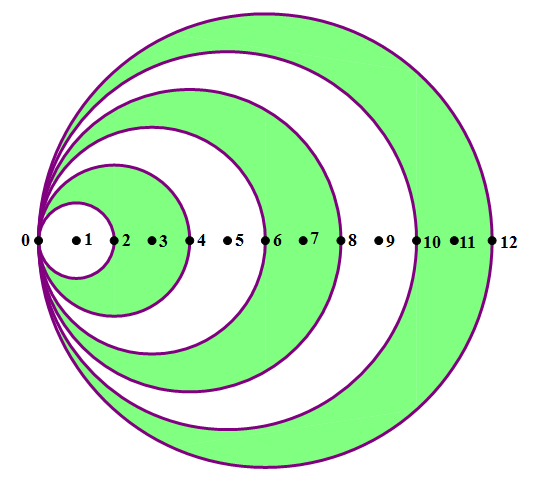
6) In the diagram above, all the points are on a line, and the number of each point indicates how many units that point is from zero. The points #1 – #6 are the centers of the six circles, and all circles pass through point zero. What is the total area of the shaded region?
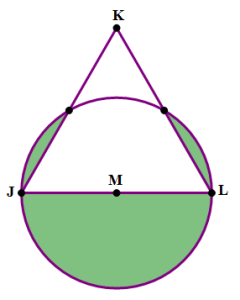
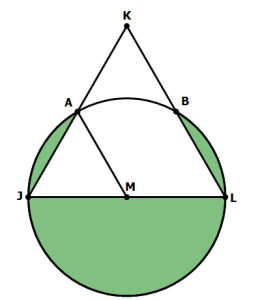
7) In the diagram above, JKL is an equilateral triangle. Point M is the midpoint of segment JL, and M is the center of a circle that passes through points J and L. The shaded regions in the diagram indicate all the regions inside the circle that are outside the triangle. What fraction of the total area of the circle is outside the triangle?
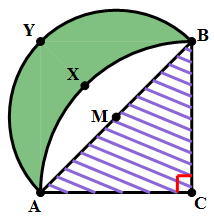
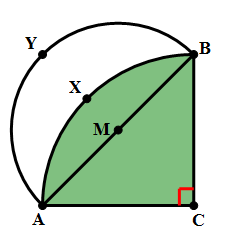
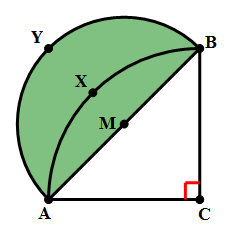
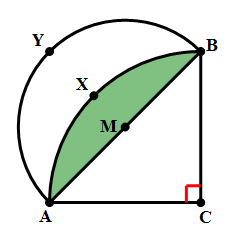
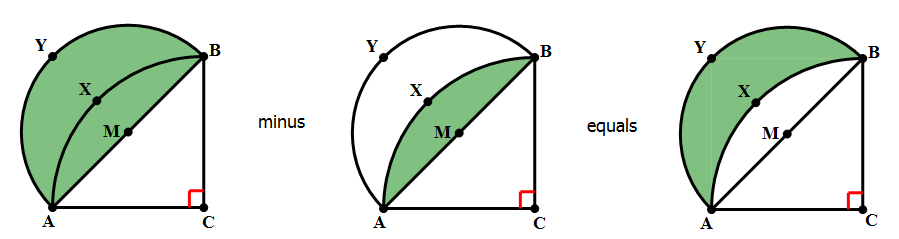
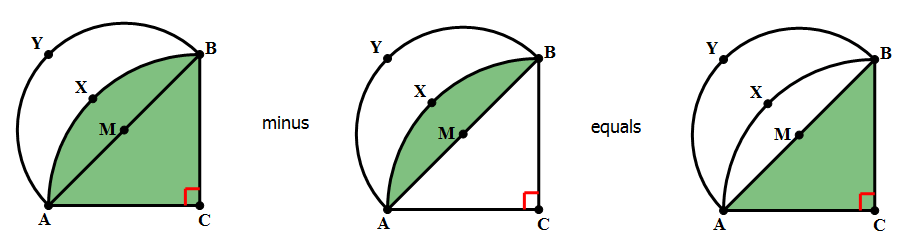
8) In the diagram above, angle C = 90º and AC = BC. Point M is the midpoint of AB. Arc AXB has its center at C, and passes through A and B. Arc AYB has its center at M and passes through A and B. The shaded region between the two arcs is called a “lune.” What is the ratio of the area of the lune to the area of triangle ABC?
Circles
Ah, the beauty of the circle, the most symmetrical of shapes! For more information about circles, see these blogs:
4) Inscribed & Circumscribed Circles
5) Circles, Arclength, and Sectors
If you have any insights while reading those blogs, you may want to give the problems above a second look. If you find any typos or anything on this page is unclear, please let us know in the comments section.
Practice problem explanations
1) First of all, we should think about the prompt a bit. This angle, 144º, is what fraction of a full circle? Well, both 144 and 360 are divisible by 4: 144 ÷ 4 = 36 and 360 ÷ 4 = 90, so
This angle is 2/5 of the whole circle, so the arc is 2/5 of the whole circumference. Also, remember that if we can find anything about the whole circle, for example, the circumference, then we can find the radius, which would allow us to find the area.
Statement #1: This is a tautological statement. A tautological statement is a statement that, by definition, has to be true, and because of this, it contains no information. Statements such as “My car is a car” and “My employer employs me” are verbal tautologies: they contain no useful information. Much in the same way, we already know from the prompt that the angle takes up 2/5 of the circle, so of course the sector would take up 2/5, or 40%, of the area. This statement repeats information in the prompt, and contains no new information, so it doesn’t help us at all to figure out anything else. This statement, alone and by itself, is not sufficient.
Statement #2: We already know this arc is 2/5 of the whole circumference, so we could set up a proportion to find the circumference. From that, we could find the radius, and that would allow us to find the area. This statement, alone and by itself, is sufficient.
Answer = (B)
2) Because ABC is an equilateral triangle, right triangle ABD is a 30-60-90 triangle, one of the GMAT favorite triangles. From the ratios of that triangle:
Half of that is radius of the circle:
Use that to find the area:
Answer = (B)
3) The fact that AB is a diameter guarantees that angle C = 90º. If we had two sides of right triangle ABC, we could find the third using the Pythagorean Theorem.
Statement #1: this gives us only one side of a right triangle: not helpful. This statement, alone and by itself, is not sufficient.
Statement #2: this allows us to solve for the radius and, hence, the diameter, so we can determine side AB. Nevertheless, this gives us only one side of a right triangle: also not helpful. This statement, alone and by itself, is not sufficient.
Combined statements: We get the length of BC from the first statement, and the length of AB from the second. Now, we have two sides of the right triangle, so we can use the Pythagorean Theorem to solve for the third side, AC. Combined, the statements are sufficient.
Answer = (C)
4) Call the radius of the larger circle y, and y = PS = ST. Call the radius of the smaller circle x, and x = RS = RQ. If we took a ratio of the areas, the factors of 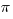 would cancel and we would be left with the ratio (y/x) squared. If we could solve for this simpler ratio, y/x, then we could find the ratio of areas.
would cancel and we would be left with the ratio (y/x) squared. If we could solve for this simpler ratio, y/x, then we could find the ratio of areas.
Statement #1: ST = y and PQ = y – 2x, so
This allows us to solve for the ratio y/x, which would allow us to find the ratio of areas. This statement, alone and by itself, is sufficient.
Statement #2: RT = y + x and PR = y – x, so
Cross-multiply.
This allows us to solve for the ratio y/x, which would allow us to find the ratio of areas. This statement, alone and by itself, is sufficient.
Answer = (D)
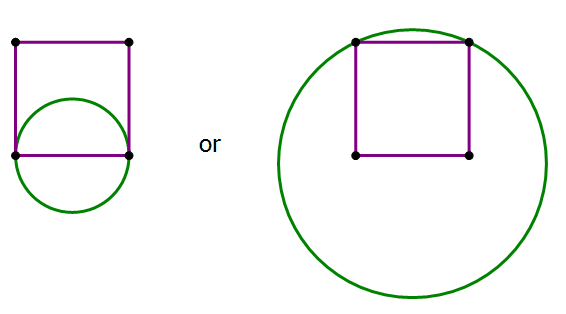
5) Statement #1: this information, with nothing more, could mean that the circle is either smaller or larger.
This statement, alone and by itself, is insufficient.
Statement #2: this information, with nothing more, could mean that the circle is either smaller or larger.
This statement, alone and by itself, is insufficient.
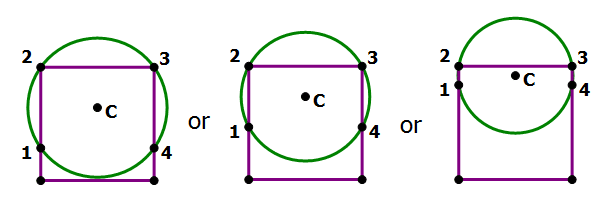
Combined Statements: One possibility is the circle that intersects the square four times by passing through all four vertices:
That circle is clearly bigger than the square. The circle absolutely cannot pass through exactly three vertices. If it pass through two vertices, it would have to intersect the side two more times. Possibilities include the following (point C is the center of the circle).
Notice that, as point C approaches the top side of the square, it gets closer and closer to the circle that has this top side as a diameter, equivalent to the first circle in the statement #1 diagram. That circle is clearly has less area than the square. Well, that circle won’t work here, because it intersects at only two points, but because point C could get closer and closer to the top side without touching it, which means the area of the circle in this diagram could get closer and closer to the area of the first circle in the statement #1 diagram. This means that we could make the circle in this diagram have less area than the square has.
Thus, even with the constraints of both statements, we can construct a circle that has an area that is either greater than or less than that of the square. Even with both statements, we cannot give a definitive answer to the prompt question. Both statements combined are insufficient.
6) First, let’s look at the outer “lobe,” the one between 10 and 12. The circle through point 12 has a center a 6 and radius of 6, so its area is 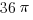 . The circle through point 10 has a center a 5 and radius of 5, so its area is
. The circle through point 10 has a center a 5 and radius of 5, so its area is 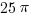 . If we subtract the latter from the former, we an area of
. If we subtract the latter from the former, we an area of 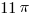 for this lobe.
for this lobe.
Now, let’s look the middle lobe, the one between 6 and 8. The circle through point 6 has a center a 3 and radius of 3, so its area is 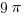 . The circle through point 8 has a center a 4 and radius of 4, so its area is
. The circle through point 8 has a center a 4 and radius of 4, so its area is 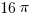 . If we subtract the latter from the former, we an area of
. If we subtract the latter from the former, we an area of 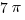 for this lobe.
for this lobe.
Now, let’s look the smallest lobe, the one between 2 and 4. The circle through point 2 has a center a 1 and radius of 1, so its area is 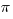 . The circle through point 4 has a center a 2 and radius of 2, so its area is
. The circle through point 4 has a center a 2 and radius of 2, so its area is 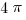 . If we subtract the latter from the former, we an area of
. If we subtract the latter from the former, we an area of 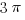 for this lobe.
for this lobe.
Add the areas of the three separate lobes: 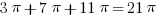 .
.
Answer = (B)
7) This is a difficult one. For the sake of argument, let’s say that JM = ML = 1. Then the area of the total circle would be 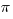 . That’s the denominator of our ratio.
. That’s the denominator of our ratio.
Clearly, part of the shaded region is the semicircle beneath JL. That part has an area of 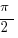 . That’s the easy part.
. That’s the easy part.
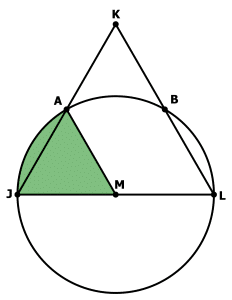
The circle intersections sides JK and KL: call these points A & B.
Point A must be the midpoint of JK, and point B, the midpoint of KL. Triangle JAM must be an equilateral triangle, with sides equal to 1. First, we will compute the area of the sector:
The angle at M is 60º, so this is one sixth of the area of the circle.
To get the area of that small shaded part, known as a circular segment, we need to subtract the area of equilateral triangle JAM from the area of the sector. See this blog for the area of an equilateral triangle.
area of segment = (area of sector) – (area of triangle JAM)
We have two circular segments, so we double this to get both:
Now, add the area of the semicircle to get the area of the whole shaded region:
Divide this by the area of the circle, 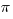 , to get the ratio:
, to get the ratio:
Answer = (E)
8) This problem is based on a famous theorem of Hippocrates of Chios (c. 470 – c. 410 BCE), a predecessor of Euclid. The easiest way to see this is as follows.
Let AC = BC = 2S. This is the radius of the larger circle, which has an area of 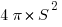 , so that the quarter circle:
, so that the quarter circle:
must have an area of 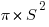 . Hold that thought.
. Hold that thought.
Now, notice that triangle ABC is a 45-45-90 triangle, so that the length of the hypotenuse must be
and the radius of the smaller circle is
The area of that whole circle would be 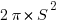 , and the area of the semicircle:
, and the area of the semicircle:
would be half of that, 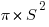 . Thus, the quarter circle of the larger circle and semicircle of the smaller circle have the same area. That’s a very big idea!
. Thus, the quarter circle of the larger circle and semicircle of the smaller circle have the same area. That’s a very big idea!
Now, look at the circular segment:
We don’t need to know that area: simply call it J.
If we subtract the circular segment, J, from the quarter circle of the bigger circle, we get the triangle:
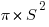 – J = area of triangle ABC
– J = area of triangle ABC
If we subtract the circular segment, J, from the semicircle of the smaller circle, we get the lune:
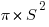 – J = area of the lune
– J = area of the lune
Because those two areas equal the same thing, they must equal each other.
area of triangle ABC = area of the lune
The two are equal, so their ratio is 1. Answer = (A)




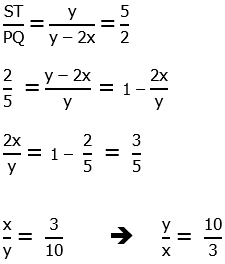
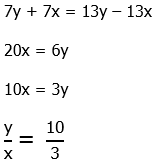
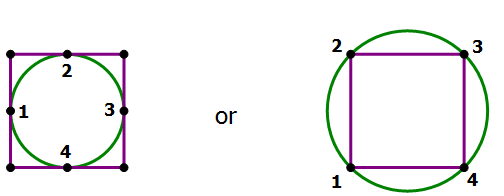




Leave a Reply