First, a few practice GMAT math questions.
1) Last year, the price of a vacation package was P. At the beginning of this year, the price went up 40%. Lucas used a travel voucher to purchase the vacation package at 30% off this year’s price. In terms of P, how much did Lucas pay?
(A) P + 10
(B) 1.1*P
(C) 1.12*P
(D) 0.9*P
(E) 0.98*P
2) Given that xy > 0, which of the following must also be greater than zero?
3) The numbers m, n, and K are all positive integers. Given that m is a factor of K, that n is also a factor of K, and m < n, which of the following must also be a positive integer factor of K?
4) Marcia took a trip consisting of three segments at three different speeds: she drove a distance of (5D) at a speed of (2v), then a distance of (4D) at a speed of (3v), then a distance of D at a speed of (6v). In terms of D & v, what was the total time of Marcia’s trip?
Answers and explanations will follow this article.
Picking numbers
It’s absolutely true that, when the GMAT gives a problem with variables in the answer choices, one possible approach is to pick numbers for the variables. Students sometimes ask, “How do I pick numbers? Can you give me a general strategy for picking good numbers in all cases?” Well, let’s start with the second question, which has a crystal clear answer: “No!” You see, there are several different kinds of questions in which picking numbers could be an appropriate strategy, and the best numbers to pick in any case depend much more on the specifics of the question. Some numbers that would be excellent choice in one question would be the worst possible choice in another question. For many questions, the best numbers to pick are inextricably tied up with the mathematics in the question itself. Some of this I will explain in the course of this article, and other things I will explain in the solution.
Numbers
First, let’s start with how you think about the word “number”. What pops into your head when I say that word? If what pops into your head is the set {1, 2, 3, 4, 5, …}, then with all due respect, you are operating with a third-grade level definition of the word “number”, and the GMAT Quant section will mercilessly punish you for such naïveté. The word “number” is a broad category, encompassing everything on the number line: zero is a number; 4/7 is a number; negative four is a number; negative one fifth is a number; pi is number; the square-root of 17 is a number; etc. etc. All of these possibilities must leap to mind when a problem mentions a “number”. It’s good to appreciate the categories of numbers, as well as their different properties.
Number sense is the ability to see patterns among numbers and sense which ones are best for a problem. The person who asks the question at the top, how to pick numbers — what that person really needs is number sense!! In other words, the person who asks for a general rule for picking numbers is really, at a very profound level, asking the wrong question. Although that person might not even be familiar with the terms, what that person really needs to develop is number sense and mathematical thinking in general. These two posts say more about these larger issues, but I will say a few general things about picking numbers here.
Percent problems
A strategy you must avoid is picking 100 for the starting value in every percent problem. Everyone has heard this strategy. Everyone who picks numbers does precisely this, as if it were a reflex. That, in a nutshell, is the problem. You see, if the test writers know that everyone makes the same choice, then they design answer choices designed to trip up people who make that all-too-obvious choice. Think a little out of the box here. Instead of 100, pick 500 or 1000 — you should be able to figure out round number percents with those relatively quickly.
Extending that strategy even a little further: if anything is a super-obvious choice to pick, then rather than pick that super-obvious thing, pick something a shade away from super-obvious.
If the question is one of a very typical type, a percent increase or decrease followed by another percent increase or decrease, then I would strongly advise against picking numbers. Instead, I would recommend using multipliers to handle percent changes.
Dimensional analysis
If different variable represent quantities of different units, then make sure you understand what combination of them will have the correct units for the answer choice. In Physics, this thinking about the units of different quantities is called dimensional analysis. For example if J is in units of miles per gallon, and M is in units of miles, then to get units of gallons, I would need M/J — if the question is asking for “how many gallons”, then the correct answer would have to be a number times M/J. Any other combinations (J/M, M*J, etc.) are automatically incorrect. This helps you eliminate answers choices, which makes the process of plugging in numbers easier.
Know the traps
Many different math questions have very predictable traps: the mistake that a large number of test takers routinely make, time and time again. GMAT problems always have answer choices that reflect these traps: in some cases, it’s as if the GMAT simply sets up a trap answer like a big butterfly net, and they watch hordes of test takers run headlong into it. For every such trap you learn to recognize and avoid, you will be that much ahead of so many other test takers.
One big trap involves a sequence of percent increases & decreases. There are a few common ones involving fractions. Still more involve exponent properties and powers. Some very common ones involve incorrect variations on three basic algebra formulas. Here’s a post on the most common math mistakes.
Avoid one
Avoid picking 1 as a value for a variable. The reason is: one has so many special properties that no other number has. For example, all powers of 1 equal one: one is the only number that has this particular property. Think if you had to distinguish choices involving different powers of that variable: picking one for the value would make all the power equal the same thing, making it impossible to distinguish which answers should be eliminated. One is often the worst possible choice.
The only exception to this is — sometimes, it’s worthwhile to pick very easy numbers, like 1 and 2, just to do a very quick elimination of a couple of answers. If that’s your goal, 1 can be a perfectly acceptable choice on a first pass. It will never be a choice that eliminate everything, but if your goal is to begin by eliminating low-hanging fruit, then by all means pick it.
To pick or not to pick
Finally, let’s step back. Why do folks pick numbers for problems with variable? One reason is that sometimes, quite rarely, one can either eliminate many answers or even get to a single right answer very quickly by picking numbers. Most often, though, this is not the case. In fact, often it’s much quicker and much easier to do the algebra directly. After all, this is precisely why mathematicians invented algebra in the first place: it’s a powerful efficient problem solving system.
Most of the time, most habitual number-pickers are choosing this strategy, not because it’s necessarily faster or easier or more efficient or better in any particular way, but simply because these folks are absolutely petrified of algebra. For these folks, algebra is a fire-breathing dragon, and folks will do anything, no matter how awkward or cumbersome, simply to avoid facing that dragon. If this describes you, then I have some hard medicine for you: do algebra. From this point forward, in any problem with variable, you are forbidden to pick numbers, and you must practice the algebra. You see, for the GMAT, you will have to know some algebra, and the only way you get better at algebra is by practicing it at every opportunity you can get.
Summary
If you had any flashes of insight while reading this article and exploring the links, you may want to give the questions at the top another look. Here’s another problem of another sort, from inside Magoosh:
5) http://gmat.magoosh.com/questions/123
Finally, if you have any questions, please let us know in the comments section at the bottom.
Practice problem explanations
1) First of all, let’s talk about the trap. Even if you don’t learn how to solve this problem, learn to recognize this trap, possibly the single most enticing trap on the entire GMAT. When a percent increase or decrease is followed by another percent increase or decrease, you cannot simply add or subtract the two percents. If you increase something by 40% and then decrease it by 30%, that is absolutely NOT a 10% increase. That is the trap answer to which hordes of GMAT test takers are drawn like bugs to a bug zapper.
Problems are this sort are not ones on which I would recommend picking numbers at all. Instead, I would recommend using multipliers for the percent changes. The multiplier for a 40% increase would be (1 + 0.40) = 1.40. The multiplier for a 30% decrease would be (1 – 0.30) = 0.70. The net effect of both would be
Final price = (1.40)*(0.70)*P = 0.98*P
Answer = (E)
Even though it’s not as efficient, here’s a picking-numbers approach, just so you can see how the numbers play out. Let p = $1000. This increases by 40%, to $1400. Now, this is going to decrease by 30% — but notice! It decreases not by 30% of the original, $1000; rather, it decrease by 30% of the new price, $1400. After the 40% increase, the price of $1000 doesn’t even exist anymore: the only price that exists at that point is the $1400 price; that’s what decreases by 30%. Well, 10% of $1400 is $140, and so, 30% = 3*10% = 3*$140 = $420. The price decrease to $1400 – $420 = $980, which is 98% of P or 0.98*P.
2) This is a /”must be true” problem. First of all, remember that if the product of two numbers is positive, either both are positive or both are negative. Since we want something that “must be greater than zero”, i.e. must be positive, I am going to pick negative numbers for my values of x & y. Probably all five answer choices would be positive if I picked to positive numbers. I am going to pick negatives, because any answer choice that winds up negative will be something I can eliminate, and on “must be true” problem, my goal is to eliminate answers.
I’ll start with very simple choices, x = –1 and y = –2.
(A) (–1) + (–2) = –3 — negative, so we can eliminate this.
(B) (+1) + (–2) = –1 — negative, so we can eliminate this.
(C) (-3)^2 + 1 = 9 + 1 = 10 — can’t eliminate yet
(D) 1 – 4 + 100 = +97 — can’t eliminate yet
(E) (-1)^2 = 1 — can’t eliminate yet
So, with one easy choice, we have eliminated two answer choices, (A) & (B). I notice that x-squared minus y-squared, in choice (D) — that expression could be negative. If it’s a small negative, then adding a hundred would make it positive, so to eliminate that, we need the subtracted term to be big. Use x = –1 and y = –30.
(D) (+1) – 900 + 100 = –799 — negative, so we can eliminate this.
Now, we are down to just (C) & (E). Notice, both of them have something in parentheses squared. Of course, if we square a positive, we get a positive, and if we square a negative, we get a positive, so it would seem that square anything gives us a positive, right? Almost. The one exception: when you square zero, you get zero, and zero is not positive. Zero is neither positive or negative. Therefore, if either of these answers could have an output of zero, then it is not always positive. Notice, if we pick x = –2 and y = –2, then the sum in the parentheses of (E) is, ((–2) – (–2)) = 0, and the sum in the parentheses of (C) is, ((–2) + (–2)) = –4
(C) +16 — can’t eliminate
(E) 0 — because zero is not positive, we can eliminate this.
In fact, if we add two negative numbers, or any two positive numbers, then we never can get zero. Therefore, the inside of the parentheses of (C) will never equal zero: it will always be a non-zero number; and therefore, when we square, it must be positive. That’s why (C) is the only possible answer.
3) First, pick a K with a lot of factors: say K = 24. Now, for m and n, pick two factors of 24 that are not factors of each other — for example, pick the two biggest factors of 24 less than 24 itself: n = 12 and m = 8
(A) 8 + 12 = 20 — not a factor of 24
(B) 8*12 = 96 — not a factor of 24
(C) (12*12)/8 = (3*12)/2 = (3*6) = 18 — not a factor of 24
(D) 24/8 = 3 — that’s a factor of 24
(E) 24/96 — not even an integer, so certainly not a factor
The only one that works is (D), the correct answer.
Notice that, in (C), to find twelve squared divided by eight, the absolute worst, most unstrategic thing one could do would be to square 12, get 144, and then have to divide that by 8 without a calculator. Notice, instead, I left the two 12’s unmultiplied while I canceled factors from the denominator, easily reducing the entire process to single-digit multiplication. Cancel before you multiply is one of the biggest non-calculator tricks on GMAT math.
4) First of all, let’s use a little dimensional analysis, discussed above. If D is a distance, and v is a speed, we know v = D*T, or T = D/v. Anything with a D in the numerator and a v in the denominator will be a time, but if those two are reversed, it will not have the right units. We can eliminate (B) & (D) right away on these grounds.
On this one, I recommend an algebraic approach.
(distance #1) = (rate #1)*(time #1)
5D = (2v)*(time #1)
time #1 = (5D)/(2v)
(distance #2) = (rate #2)*(time #2)
4D = (3v)*(time #2)
time #2 = (4D)/(3v)
(distance #3) = (rate #3)*(time #3)
D = (6v)*(time #1)
time #3 = (D)/(6v)
TOTAL TIME = (time #1) + (time #2) + (time #3)
= (5D)/(2v) + (4D)/(3v) + (D)/(6v)
= (D/v)[5/2 + 4/3 + 1/6]
= (D/v)[15/6 + 8/6 + 1/6]
= (D/v)[24/6]
= (D/v)[4]
= (4D)/v
Answer = (A)
While it’s somewhat less efficient, here’s a picking number approach. We want D to be a number with lots of factors, including a factor of 6, because it’s going to be divided by 2 and 3 and 6 times something. Let’s pick D = 60 and v = 10
First leg: distance = 5D = 300 mi, at a speed of 2v = 20 mph, that’s T = D/V = 300/20 = 15 hours.
Second leg: distance = 4D = 240 mi, at a speed of 3v = 30 mph, that’s T = D/V = 240/30 = 8 hours.
Third leg: distance of D = 60 mi, at a speed of 6v = 60 mph —that will take exactly one hour.
TOTAL TIME = 15 hr + 8 hr + 1 hr = 24 hours
Well, D/V = 60 mi/10 mph = 6 hours, and clearly, we need to multiply this by 4 to get 24 hours, not by 10/11 or 11/10, so (A) is the answer.

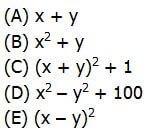
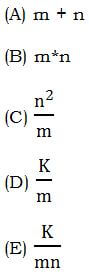
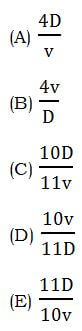





Leave a Reply