First, here are two challenging GMAT algebra problems, both involving three equations with three algebraic unknowns.
2a + b + 3c = 6
a – b + 5c = 12
3a + 2b + 2c = 2
1) Given the equations above, what does the product a*b*c equal?
-
(A) 6
(B) -6
(C) 12
(D) -12
(E) 24
6x – 5y + 3z = 23
4x + 8y – 11z = 7
5x – 6y + 2z = 12
2) Given the equations above, x + y + z = ?
-
(A) 11
(B) 12
(C) 13
(D) 14
(E) 15
Full solutions will follow this article.
Simplifying
In a previous post, I discussed solving two algebra equations with two unknowns. That’s already a challenging task. Three equations with three unknowns is even trickier, and something you are quite unlikely to see unless you are already performing brilliantly on the Quant section.
Well, it turns out, solving these, we use a time-honored problem-solving strategy: inside every big problem is a little problem struggling to get out. Yes, that’s playfully stated, but I have found it is often surprisingly apt in all kinds of personal and interpersonal situations.
What’s considerably more pertinent here — this basic idea is the core of much advanced mathematical thinking, at the levels of calculus, analysis, number theory, and other more abstruse topics. At all levels, mathematicians strive to reduce problems which they don’t know how to solve to problems which they do know how to solve. That can be a hugely valuable perspective on GMAT mathematical strategy. Among other things, that’s precisely the approach with these problems. I will assume you have read that previous post and are somewhat competent in the two variable/two equation problems — for the purposes of this discussion, I will consider those the problems we do know how to solve. I will also assume you are familiar with substitution and elimination from that previous post.
The approach
Here’s the general strategy for solving three equations with three unknowns.
Step #1: Pick a pair of equations, two of the three, and using either substitution or elimination, eliminate one of the variables. Most often, elimination is much much easier than substitution! After this step, we will end up with one equation with two unknowns.
For this one, you have to step back and have your right-brain pattern matching hat on. You have to think very strategically about what would be the most efficient. For example, in problem #1 above, if I wanted to pick the first two equations and eliminate c, I could do that, but it would involve multiplying the first equation by 5 and the second equation by (-3), which would lead to some big numbers. Hmmm. Not the slickest approach. Instead, when I look at these equations I notice —- the first equation has a (+b) and the second equation has (-b), so without any fuss, I could add those equations and right away eliminate b. That’s a considerably more efficient approach.
Step #2: Pick a different pair of equations, and through elimination, eliminate the same variable you eliminated in step #1. As the result of this step, we now will have two equations with the same two unknowns.
Step #3: At this point, we have reduced the problem we didn’t know how to solve to one we do know how to solve: two equations with two unknowns. Use those techniques to solve for those two variables.
Step #4: Once you have the numerical values of two of the variable, plug into any of the original equations to solve for the value of the third variable.
I will demonstrate this entire strategy in the solution to #1 below.
Do I have to solve?
For problem #1 above, we have to solve fully, but the coefficients are reasonably small, and as it turns out, the numbers come out nice and neat. By contrast, #2 is a monster. The numbers are larger and uglier, and the answer will come up as ugly fractions. But, as it turns out, we can answer the questions being asked with only a minimum of calculations.
This is where you really have to have your creative, out-of-the-box, right brain cap on. Question #2 is not asking for the values of individual variables, but for an expression. As it turns out, there’s an unbelievably simple way to jump directly to the answer with astonishingly little work. Do you see it? I will discuss this in the solution below.
The Moral: Don’t automatically assume you always have to slog through the hard work of solving for all the individual variables. Always keep your antennae up for creative, time-saving shortcuts!
Summary
Once again, these problems are very rare. You will not see them at all unless you are performing at 700+ level, getting almost everything else right. Here’s another problem, for further practice:
3) http://gmat.magoosh.com/questions/1009
If you have any questions on what I’ve said here, let me know in the comments sections below!
Solutions to practice problems
1) Here, I will show the full solution outlined above. First of all, here are the equations, with letter designations.
(P) 2a + b + 3c = 6
(Q) a – b + 5c = 12
(R) 3a + 2b + 2c = 2
(I started later in the alphabet, so these letter-names of the equations wouldn’t be confused with answer choice letters!) First of all, I notice that lovely (+b) in (P) and (-b) in (Q), so I will add those two.
That is new equation (S), with variable a & c. Now, in step #2, we want to pick a different pair of equations, and eliminate the same variable, b. Again, I like the (-b) in (Q) — that won’t be hard to use to cancel (+2b) in equation in (R). Just multiply (Q) by 2, and add it to (R).
Now, with (S) and (T), we have two equations with the same two unknowns, a & c. The numbers 8 & 24, the coefficients of c, have a LCM of 24. Multiply (S) by 3 and (T) by (-2).
Thus, a = -2. Plug this value into (S).
Plug these two values into (P).
Thus, {a, b, c} = (-2, 1, 3), and their product a*b*c = -6. Answer = (B).
2) As with the last problem, I will begin by giving letter names to the equations.
(P) 6x – 5y + 3z = 23
(Q) 4x + 8y – 11z = 7
(R) 5x – 6y + 2z = 12
Here, it would be a colossal waste of time to solve for the individual values of x & y & z separately. We want to find the value of x + y + z. Notice, first of all, that the x-coefficient of (R) is one higher than that of (Q); unfortunately, their y-coefficients are 14 units apart from each other, not close at all. Now, notice that the x-coefficient of (P) is one higher than that of (R); also, the y-coefficient of (P) is one higher than that of (R); also, the z-coefficient of (P) is one higher than that of (R)! BINGO! The difference, (P) – (R), equals the expression we seek!
Answer = A


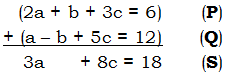
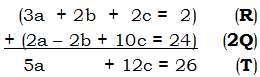
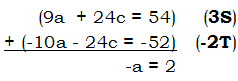
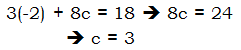
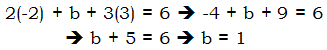
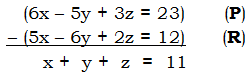




Leave a Reply