Here is a set of 11 GMAT probability questions, all in the Problem Solving style on the test, collected from a series of blog articles. Answers and links to explanations to these these GMAT probability problems are at the end of set.
——————————————————————————————————————————————
The scenario below is relevant to questions #1-#3.
There are two sets of letters, and you are going to pick exactly one letter from each set.
Set #1 = {A, B, C, D, E}
Set #2 = {K, L, M, N, O, P}
1) What is the probability of picking a C and an M?
-
(A) 1/30
(B) 1/15
(C) 1/6
(D) 1/5
(E) 1/3
2) What is the probability of picking a C or an M?
-
(A) 1/30
(B) 1/15
(C) 1/6
(D) 1/5
(E) 1/3
3) What is the probability of picking two vowels?
-
(A) 1/30
(B) 1/15
(C) 1/6
(D) 1/5
(E) 1/3
————————————————————————————————————————————
Set #1 = {A, B, C, D, E}
Set #2 = {K, L, M, N, O, P}
4) There are these two sets of letters, and you are going to pick exactly one letter from each set. What is the probability of picking at least one vowel?
-
(A) 1/6
(B) 1/3
(C) 1/2
(D) 2/3
(E) 5/6
5) Suppose you flip a fair coin six times. What is the probability that, in six flips, you get at least one head?
-
(A) 5/8
(B) 13/16
(C) 15/16
(D) 31/32
(E) 63/64
6) In a certain game, you pick a card from a standard deck of 52 cards. If the card is a heart, you win. If the card is not a heart, the person replaces the card to the deck, reshuffles, and draws again. The person keeps repeating that process until he picks a heart, and the point is to measure: how many draws did it take before the person picked a heart and won? What is the probability that one will have at least three draws before one picks a heart?
-
(A) 1/2
(B) 9/16
(C) 11/16
(D) 13/16
(E) 15/16
7) Five children, Anaxagoras, Beatrice, Childeric, Desdemona, and Ethelred, sit randomly in five chairs in a row. What is the probability that Childeric and Ethelred sit next to each other?
-
(A) 1/30
(B) 1/15
(C) 1/5
(D) 2/5
(E) 7/20
8) John has on his shelf four books of poetry, four novels, and two reference works. Suppose from these ten books, we were to pick two books at random. What is the probability that we pick one novel and one reference work?
-
(A) 1/2
(B) 2/5
(C) 3/10
(D) 7/20
(E) 8/45
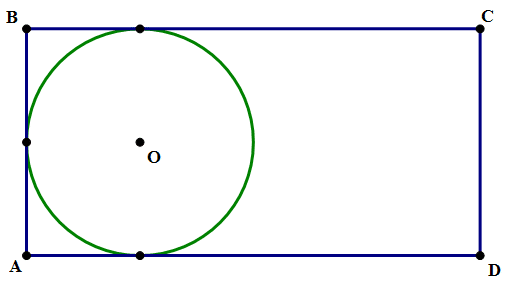
9) In the diagram above, the sides of rectangle ABCD have a ratio AB:BC = 1:2, and the circle is tangent to three sides of the rectangle. If a point is chosen at random inside the rectangle, what is the probability that it is not inside the circle?
10) Region R is a square in the x-y plane with vertices J = (–1, –2), K = (–1, 4), L = (5, 4), and M = (5, –2). What is the probability that a randomly selected point in region R lies below the line 3x – 5y = 10?
-
(A) 5/12
(B) 5/18
(C) 5/24
(D) 5/36
(E) 5/72
11) In the diagram above, WZ = XZ, and circular arc XY has a center at W. If a point is selected from anywhere within this figure, what is the probability that it is selected from the shaded region?
Summary
If you have comments or questions, please let us know in the comment section at the bottom! 🙂
Answers
1) A
2) E
3) B
4) C
5) E
6) B
7) D
8) E
9) D
10) C
11) A
Explanations
For the explanations for #1-3, see this post.
For the explanations for #4-6, see this post.
For the explanations for #7-8, see this post.
For the explanations for #9-11, see this post.
Check out this post if you want a wider range of Problem Solving sample questions.


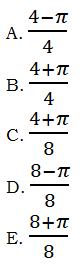

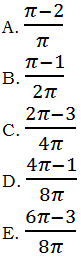




Leave a Reply