Attention, mad scientists out there! Consider these two practice questions.
1) A scientist has 400 units of a 6% phosphoric acid solution, and an unlimited supply of 12% phosphoric acid solution. How many units of the latter must she add to the former to produce a 10% phosphoric acid solution?
(A) 200
(B) 400
(C) 500
(D) 600
(E) 800
2) A chef mixes P ounces of 60% sugar solution with Q ounces of a 10% sugar solution to produce R ounces of a 25% sugar solution. What is the value of P?
[Statement #1] Q = 455 mL
[Statement #2] R = 660 mL
Mixtures, solutions, and concentration
First of all, keep in mind: this is relatively rare kind of GMAT Math problem. There’s a good chance you could take five GMATs in row and never see a mixture problem. Nevertheless, they do arise occasionally, and it’s good to be familiar with them.
Let’s think for a moment about “concentration” — not the mental quality, but in the chemical solution sense. What does it mean to say we have a “400 units of a 6% phosphoric acid solution”? Whatever those units are, the total amount of mixture, of solution, we have is 400 units, and of that, 6% is pure phosphoric acid. Well, 6% of 400 is 24, so we know we have 24 units of pure phosphoric acid. That is the amount of concentrate we have in our solution. (Those “units” could be units of volume or units of mass, but that’s far more detail that you need to know on the GMAT).
I bet “phosphoric acid” sounds highly technical and abstruse: it’s actually one of the ingredients listed on every can of Coca Cola.
The two equations
The secret to any mixture or concentration problem is to use the two equations. First is the amount of stuff, the total volume. This is called the volume equation. The basic idea is:
This makes sense when you think about it: the volume of the resultant solution had to come from the volumes of the two things we mixed.
The second equation is similar. This concerns, specifically, the amount of concentrate, of whatever the chemical or substances is of which we have a solution. In problem #1, the concentrate is phosphoric acid, and in problem #2, sugar. The amount of concentrate that winds up in the resultant solution must come from somewhere. It must come from the amount of concentrate in the two solutions mixed.
As in the section above, these amounts of concentrate will always be (the concentration percentage) times (the total volume of the solution concerned).
If you had trouble with the problems above before, go back to them, and see if you can set up both of these equations and solve. Give them another try before reading the explanations below.
Also, here’s another practice question:
3) http://gmat.magoosh.com/questions/29
Practice problems explanations
1) We could backsolve from the numerical answer choices, but let’s use a straight algebra approach. Let X equal the units of 12% phosphoric acid solution we use, and let Y be the units of 10% sulfuric acid solution that result.
The volume equation is:
400 + X = Y
In the first solution, we have 6% of 400, or 24 units of phosphoric acid.
In the second solution, we have 12% of X = 0.12*X of phosphoric acid.
In the resultant solution, we have 10% of Y = 0.10*Y of phosphoric acid.
The concentration equation is:
24 + 0.12*X = 0.10*Y
Multiply this by 100, to clear the decimals:
2400 + 12X = 10Y
Everything is even, so divide by 2 to simplify:
1200 + 6X = 5Y
We want X, so let’s multiply the volume equation by -5 and add that to this equation we just got:
Answer = E
2) This one is very elegant. We have three variables — the amount of 60% sugar solution, the amount of 15% sugar solution, and the amount of the resultant 25% sugar solution. Three variables. We have two equations: the volume equation and the concentration equation. Right now, three variables and two equations: we can’t solve.
Now, look at the statements. Each statement gives us the value of one of the variables. If we get the value of one variable, that’s no longer a variable, and thus we are down to two variables with two equations: that’s a situation in which we can find a full solution. Thus, given the value of either Q or R, we enter a situation in which we can solve for everything, and thus we would know P. Therefore, each statement, by itself, is sufficient. Answer = D




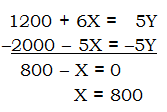




Leave a Reply