GMAT Shortcut: Adding to the Numerator and Denominator

Mike MᶜGarry

August 6, 2012

GMAT Data Sufficiency

First, try these practice DS questions:

1) If x and y are positive integers, is ?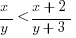

Statement #1: y > 20
Statement #2: x < 5

2) If x and y are positive integers, is ?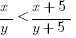

Statement #1: y = 5
Statement #2: x > y

Throughout this post, assume that I am talking about positive fractions with a positive numerator and positive denominator. If the fraction is negative, use the information below to figure out what happens to the absolute value of the fraction, and judge from there.

Adding and Subtracting

Ironically, it’s a bit easier if we add to part of the fraction and subtract from the other.

The BIG idea here: if you increase the numerator and/or decrease the denominator of any positive fraction, that fraction will get bigger; if you decrease the numerator and/or increase the denominator of any positive fraction, that fraction will get smaller.

Add a positive number to the numerator and/or subtract a positive number from the denominator of any positive fraction, and the new fraction will be greater than the starting fraction. Subtract a positive number from the numerator and/or add a positive number to the denominator of any positive fraction, and the new fraction will be smaler than the starting fraction. Though not relevant in the two practice problems above, this is a golden rule that will help you in a panoply of fraction and ratio problems.

Adding the Same Number to Numerator and Denominator

Suppose we start with the positive fraction x/y and we want to add some positive number b to both the numerator and the denominator. How does the resultant fraction, (x + b)/(y + b), compare to the starting fraction?

Well, the rule here is a bit subtle. When you add the same number to numerator and denominator, the resultant fraction is closer to 1 than is the starting fraction. This means, if the starting fraction x/y is less than 1, then the resultant fraction is closer to one — bigger than the starting fraction. If the starting fraction x/y is an “improper fraction”, a fraction with a value greater than one, than adding the same number to both the numerator and the denominator will make the resultant fraction closer to 1 — less than the starting fraction.

Here are a couple of examples.

Example #1

Start = 2/3 —- a fraction less than one.

Add five to the numerator and the denominator.

Result = 7/8 — this fraction is closer to one than is 2/3: on the number line —–

Since 1 is bigger than 2/3, when the resultant fraction moved closer to 1, it got bigger than 2/3. Therefore, we know 2/3 < 7/8

Example #2

Start = 3/2 —- a fraction greater than one.

Add two to the numerator and the denominator.

Result = 5/4 — this fraction is closer to 1 than is 3/2: on the number line —–

Since 1 is less than 3/2, when the result fraction moved closer to 1, it got smaller than 3/2. Therefore, we know 3/2 > 5/4

Adding Different Numbers to the Numerator and Denominator

Actually, this case is simply a generalization of the previous case. Suppose we start with a fraction x/y, and we add the positive number a to the numerator and the positive number b to the denominator, and we want to know if the resultant fraction is bigger or smaller than the starting fraction.

Well, the general rule is: adding a to the numerator and b to the denominator moves the resultant fraction closer to the fraction a/b. If x/y < a/b, moving the starting fraction close to a/b will make it bigger. If x/y > a/b, moving the starting fraction close to a/b will make it smaller.

Here are some example:

Example #3

Start = 2/7

Add 3 to the numerator and 5 to the denominator.

Resultant fraction = 5/12— this fraction is closer to 3/5 than is 2/7 —-

On the number line —–

Because 3/5 is bigger than 2/7, adding 3 to the numerator and 5 to the denominator has the net effect of producing a fraction that is bigger: 2/7 < 5/12

Example #4

Start = 11/12

Add 2 to the numerator and 5 to the denominator.

Resultant fraction = 13/17— this fraction is closer to 2/5 than is 11/12 —-

On the number line —–

Because 2/5 is less than11/12, adding 2 to the numerator and 5 to the denominator has the net effect of producing a fraction that is smaller: 11/12 > 13/17

Now that you know these rules, go back to the practice problems at the beginning and see whether they make more sense now.

Practice Problem Solutions

1) Statement #1: We are adding 2 to the numerator and 3 to the denominator, so we know the resultant fraction will move closer to 2/3. If all we know is that the denominator of the starting fraction is greater than 20, then we have no idea what the size of the starting fraction is: it could be much greater than 2/3, or much smaller than 2/3, depending on the numerator, of which we have no idea. We can draw no conclusion right now. This statement, alone, by itself, is insufficient.

Statement #2: Now, all we know is that the numerator of the starting fraction is less than 5 — it could be 4, 3, 2, or 1. We have no idea of the denominator. If y = 50, then we get a very small fraction. But if x = 4 and y = 1, the fraction equals 4, much larger than 2/3. In this statement, we have no information about the denominator, and since we know nothing about the denominator, we know nothing about the size of the starting fraction: it could be either greater or less than 2/3. Therefore, we can draw no conclusion. This statement, alone, by itself, is also insufficient.

Now, combine the statements. We know y > 20 and x < 5. Well no matter what values we choose, we are going to have a denominator much bigger than the numerator. The larger possible fraction we could have under these constraints would be 4/21 (largest possible numerator with smallest possible denominator). The fraction 4/21 is much smaller than 1/2, so it’s definitely smaller than 2/3. Any fraction with y > 20 and x < 5 will be less than 2/3. Therefore, adding 2 to the numerator and 3 to the denominator will move the resultant fraction closer to 2/3, which has the net effect of increasing its value. Therefore, the answer to the prompt question is “yes.” Because we can give a definite answer to the prompt, we have sufficient information.

Neither statement is sufficient individually, but together, they are sufficient. Answer = C.

2) We are adding the same number, 5, to both the numerator and the denominator, so the value of x/y will move closer to 1. All we need to determine is whether x/y is greater than 1 or less than 1.

Statement #1: y = 5. Here, we have a definite value for y, but zero information about x. If y = 5, some fractions (1/5) can be less than one, while others (7/5) will be greater than one. Either is possible. Since both are possible, we can’t give a definitive answer to the prompt. This statement, alone, by itself, is insufficient.

Statement #2: x>y. Dividing both sides of this inequality by y, we get (x/y) > 1. This means x/y must be a fraction greater than 1, which means the resultant fraction (x + 5)/(y + 5) must be closer to one, which means the resultant fraction must be smaller. Therefore, we can definitively say: the answer to the prompt question is, “No.” Because we can give a definite answer to the prompt, we have sufficient information. This statement, alone, by itself, is sufficient.

Statement #1 is insufficient and Statement #2 is sufficient. Answer = B.

Author

Mike MᶜGarry

Mike served as a GMAT Expert at Magoosh, helping create hundreds of lesson videos and practice questions to help guide GMAT students to success. He was also featured as “member of the month” for over two years at GMAT Club. Mike holds an A.B. in Physics (graduating magna cum laude) and an M.T.S. in Religions of the World, both from Harvard. Beyond standardized testing, Mike has over 20 years of both private and public high school teaching experience specializing in math and physics. In his free time, Mike likes smashing foosballs into orbit, and despite having no obvious cranial deficiency, he insists on rooting for the NY Mets. Learn more about the GMAT through Mike’s Youtube video explanations and resources like What is a Good GMAT Score? and the GMAT Diagnostic Test.

View all posts

Share1

Comments

36 responses to “GMAT Shortcut: Adding to the Numerator and Denominator”

Vinisha Khara

September 6, 2017

If x and y are positive integers, is {x/y} y

Here why can’t we combine both the statements.

For example:
x/y = 6/5 (x>y)
Result: 6+5/5+5 = 11/10
Since 1 is less than 6/5, when the result fraction moved closer to 1, it got smaller than 6/5.Therefore, we know 6/5 > 11/10.

The ans for this could be C.

Reply
1. Magoosh Test Prep Expert
  
  September 9, 2017
  
  While we could use statement 1 to plug in 5 for y and get a hypothetical solution to this problem, we don’t absolutely need to. And without Statement 2, Statement 1 is simply insufficient. So the answer would still be (B).
  
  Reply
  1. asma sattar
    
    February 26, 2018
    
    hi
    i soled the question same as vinisha solved it and not able to understand your reply properly. please elaborate it more that why answer is B rater than C or D. Thanks
    
    Reply
    1. Magoosh Test Prep Expert
      
      March 6, 2018
      
      I’ll b happy to explain further, Asma. 🙂 First let’s look at answer C.
      
      Answer C says that “BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.” While it is true that you could combine (1) and (2) together to get an answer, you could also get an answer just based on (2). So it’s not accurate to say “NEITHER statement ALONE is sufficient.” (2) alone is sufficient, so the second half answer (C) is clearly not true.
      
      Now, let’s look at choice (D). (D) says that “EACH statement ALONE is sufficient to answer the question asked.” But this also isn’t true. Why? Because if statement 1 is truly ALONE, then you don’t have statement 2. And without statement 2, statement 1 can provide a result that is less than one (such as 2/5), or a result that is more than 1 (such as 200/5). (You can see two other >1/<1 results in Mike’s text explanation in the blog post. Statement 1 only necessitates a solution greater than 1 if you have read statement 2 and thus know for a fact that x/y > 1 (Again, see Mike’s text explanation in this post for the algebraic steps that turn statement to into x/y>1.) Since Statement 1 does not get a definite answer unless combined with statement 2, you can’t say that EACH statement alone is sufficient. One of the statements alone– statement 1, is insufficient in isolation.
      
      Reply
Zachary

November 9, 2016

Can you please explain the algebra behind if you add (p/q) to (a/b) then the sum will be closer to (p/q)?

Reply
1. Magoosh Test Prep Expert
  
  November 16, 2016
  
  I’ll be happy to explain this. What you’re asking about is a very important principle for comparing fractions.
  
  First off, it’s not quite accurate to say that if you add fraction (p/q) to (a/b), the sum will be closer to (p/q) than (a/b). This is not necessarily true, and the real rule is a little more complicated than that.
  
  The actual rule is that if you start with fraction (a/b) and then change it to (a+p)/(b+q), the resulting fraction will be closer to the fraction (p/q). But it’s important to remember that the operation (a+p)/(b+q) is NOT the same as the operation (a/b)+(p/q).
  
  To illustrate this difference and how it works, let’s plug in some numbers for the values a, b, p, & q:
  
  a= 1
  b = 2
  c = 3
  d = 4
  (We’re going with some pretty simple values here, but the algebra principle in question will hold true no matter which values we uses.)
  
  OK, now let’s plug in the numbers for (a+p)/(b+q):
  
  (1+3)/(2+4) = 4/6 = 2/3
  
  Compare this to the operation (a/b)+(p/q) with the numbers plugged in:
  (1/2)+(3/4) = (2/4)+(3/4) = 5/4
  
  Note that we get two completely different answers here. This, again, is because (a+p)/(b+q) is a completely different operation than (a/b)+(p/q). It’s the former operation– (a+p)/(b+q) that brings the original fraction (a/b) closer to fraction (p/q).
  
  You can see this is true if you compare the values of (a/b), [(a+b)/(p+q)], and (p/q). Let’s take a look:
  
  (a/b) = 1/2
  [(a+b)/(p+q)]= 2/3
  p/q = 3/4
  
  For easy comparison, let’s now express these numbers in terms of 12ths, their lowest common denominator:
  
  (a/b)= 1/2= 6/12
  [(a+b)/(p+q)]= 2/3 = 8/12
  (p/q) = 3/4 = 9/12
  
  Notice that 8/12 is closer to the p/q value of 9/12, compared to the original a/b value of 6/12.
  
  This will always hold true. If you add one number to the numerator of a fraction and another number to the denominator of the fraction, the resulting number will be closer to the ratio of what you added to the top and bottom. Just remember that to apply this rule, you add numbers to the numerator and denominator of a fraction separately. You don’t simply add new fractions.
  
  Reply
Kristin

March 2, 2016

Why didn’t you compare 6/200 to 7/235 for the last question, and cross multiply?

Reply
1. Magoosh Test Prep Expert
  
  March 6, 2016
  
  Hi Kristin,
  
  Happy to help! 🙂 There are two ways to approach this problem:
  
  Compare the old ratio to the ratio of new people only. This is what we did with 6/200 and 1/35.
  Compare the old ratio to the ratio of all people (old and newly arrived). This is what you would have done if you compared 6/200 and 7/235
  
  Both allow us to find the answer, but the former eliminates the need for calculation or cross multiplication. If the second approach makes more sense to you, that’s okay! It’s perfectly valid. Just to be clear, we are not saying that anyone has left the school using the method we’ve used.
  
  Now, let’s look at the actual decimal values of each of these:
  
  6/200 = 0.03
  1/35 = 0.0286
  7/235 = 0.0298
  
  You can see that 1/35 is smaller than 6/200. There is a small but important difference between 6/200 and 7/235, though. You have mixed the two values of the original population and new population; 7/235 is actually smaller! (Just barely.) This makes sense because we added 1/35 which is a smaller ratio of teachers to students, so it brought the overall ratio down for the whole population. This is why we can choose to look at just 1/35 instead of the entire 7/235, but both lead to the same conclusion. We know that adding a ratio with a smaller teacher:student relationship will bring down the value it is added to (just slightly).
  
  You do not have to reduce the fractions as we did–simple cross-multiplication of the old and new population would have worked just fine. Likewise, we could have also cross multiplied the original population and newly arrived. Even still, if you were good at approximating in your head, you could have left 3/100 where it was and compared using number sense if you were comfortable.
  
  I hope that helps!
  
  Reply
Amy

January 27, 2016

Hi Mike,
Thanks so much for your lessons. It’s been quite a while since most of this. That being said, in the first example in you video, 4/5 ?? 104/205, could I just have seen that 1/2 was added and then cross multiplied to arrive at 8 > 5 so 4/5 > 104/205?

Reply
1. Magoosh Test Prep Expert
  
  February 14, 2016
  
  Hi Amy,
  
  Sorry for the late reply!
  
  I would not instruct someone to use your method, but your intuition is correct. Because 104/205 is very close to 1/2, we could quickly compare 4/5 to 1/2 and realize that 4/5 is the larger of the fractions. Nice work! 🙂
  
  Reply
Sophie

November 10, 2015

Hi Mike,
Thanks for writing some of the best GRE/GMAT math content out there.

Was wondering about this sentence: “Add a positive number to the numerator and/or subtract a positive number from the denominator of any positive fraction, and the new fraction will be greater than the starting fraction.”

I think I have a counterexample: the positive fraction 4/3, if we added 2 to the numerator and subtracted 4 from the denominator. The result, of course, would be -6, which is definitely less than 4/3. What gives?

Thanks,
Sophie

Reply
1. Sophie
  
  November 10, 2015
  
  Also, would it be fair to say that action on the denominator carries more weight (all other things being equal)? In other words, adding 4 to the numerator and subtracting 5 from the denominator is going to give you a bigger number than adding 5 to the numerator and subtracting 4 from the denominator. ?
  
  Thanks!
  
  Reply
Maryanne Kamunya

October 11, 2015

Dear Mike

Oh word. please ignore my question, i totally understand now, where the 1/2 comes into effect. Your answer to Ali was VERY HELPFUL!

ALSO THANKS FOR OPENING ME UP TO SIMPLE AND FUN WAYS OF UNDERSTANDING MATHS. Im really enjoying all your reasons.

Kind regards from Kenya :0)

Reply
Maryanne Kamunya

October 11, 2015

Oh wait. Are you using 1/2 because it’s the middle ground between 0-1 on the number line? Seeing that we don’t know what the original fraction is, we would have to presume a middle ground?

Reply
Maryanne Kamunya

October 11, 2015

Hey there Mike. I was following your explaination and understood everything, until this part.

“The fraction 4/21 is much smaller than 1/2, so it’s definitely smaller than 2/3.”

Where in the world do you get 1/2 from?

I understand why 4/21 is smaller than 2/3: if you use the idea of division. dividing anything by 21 people vs 3 people, the people in the latter fraction get more of the product than in the first fraction.

Reply
Malaiya

October 3, 2015

Hi Mike,

I am taking Magoosh course and was going through this lecture. Though, it’s a very nice trick of adding and subtracting from a given fraction to find out which fraction is greater/smaller, I found it little difficult to understand/remember. So I represented it in similar/simpler terms (as below) for my understanding. I need your help to understand, if this is correct?

For positive numbers:

a/b ?? x/y
is same as: a/b ?? (x-a)/(y-b)

This will help reduce RHS towards getting simpler form and now we can apply cross multiplication to find which number is greater/smaller.

Reply
1. Mike McGarry
  
  October 6, 2015
  
  Dear Malaiya,
  I’m happy to respond. 🙂 Unfortunately, my friend, those two lines are not equivalent. Consider the following:
  a/b = 1/17
  x = y = 3/5
  Clearly, (a/b) < (x/y)
  Notice that
  (a – x)/(b – y) = (1 – 3)/(17 – 5) = (-2)/(12) = -1/6
  Well, (-1/6) is LESS than (+1/17), because any positive is greater than any negative. I am not sure what steps you used to concoct that formula, but it is simply not correct. The formula as you have written it does not work.
  The ideas of that video lesson are hard: if it were possible to sum up what I was communicating in a simple formula, I would have done so. Nothing in the Magoosh lesson or VEs is harder than it has to be. If you encounter something hard, and think you can replace it with something easy, be suspicious of what you have found. We are not keeping any easy secrets from you! 🙂
  Does all this make sense?
  Mike
  
  Reply
  1. Sami
    
    December 26, 2015
    
    Hi Mike
    
    I looked into example # 2 above for adding the same number to numerator and the deliminator. 3/2+2/2= 5/2 NOT 5/4 as stated in the example! and 5/2 >3/2
    
    please explain
    
    Reply
Simeon

April 22, 2015

There seems to be a typographical error in the third paragraph under the ‘Practice Problem Solutions’ heading :

“Now, combine the statements. We know y > 20 and x < 5. Well no matter what values we choose, we are going to have a denominator much smaller than the numerator."

Shouldn't that last sentence read "…we are going to have a denominator much BIGGER THAN the numerator" ?

Reply
1. Mike
  
  April 23, 2015
  
  Dear Simeon,
  YES! That’s perfectly correct! Thank you! 🙂 That was a typo, and I just fixed it. Your sharp eye for detail will serve you very well on the GMAT. Best of luck!
  Mike 🙂
  
  Reply
ali

April 21, 2015

I am confused s to how you place numbers like 13/17, 11/12, 2/5 on the number line. I mean how do you position them. Like on a number line between o and 1 where and how will I put 13/17. Do I have to divide the section in 17 parts then count till the 13th part and mark it?. This takes a lot of time. Or is there a simpler way. Thanks – See more at: https://magoosh.com/gmat/2012/gmat-shortcut-adding-to-the-numerator-and-denominator/#comment-1658493

Reply
1. Mike
  
  April 23, 2015
  
  Dear Ali,
  I’m happy to respond. My friend, you are thinking too literally about 13/17. You have to use number sense. Number sense is the ability to use the patterns of numbers. It’s the ability to think creatively, outside-of-the-box, to use these patterns for efficient problem-solving.
  Suppose I had to place (13/17) and (11/12) and (2/5) in order, smallest to biggest. Figuring out the exact position of each one separately is a colossal waste of time. First of all, notice that (13/17) and (11/12) are bigger than (1/2) because the numerators are more than half of the denominator, and (2/5) is less than (1/2), because 2 is less than half of 5. Thus, two of the fractions are greater than (1/2), so the one that is less than (1/2) must be the smallest. You should be able to see that very quickly.
  Now, I notice that (11/12) is very close to 1: it is only (1/12) less than one. Meanwhile, (13/17) is (4/17) less than one. Well, it’s easy to compare (1/12) and (4/17). Notice that (4/17) is almost as big as (1/4), which is much larger than (1/12). Another way to say it is
  (4/17) > (4/20) = (1/5) > (1/12)
  So, (11/12) is much closer to one, so it must be bigger than 13/17. Thus,
  (2/5) < (13/17) (12/18) = (2/3)
  Similarly, if we added one to the numerator and subtracted one from the denominator, the fraction would get bigger.
  (13/17) < (14/16) = (7/8)
  This simple trick immediately tells us that (13/17) must be between (2/3) and (7/8). That is super-precise estimation. I thought to do this, adding & subtracting 1, because both the numerator and denominator of (13/17) are odd, so I knew adding and subtracting 1 would produce two even numbers, so something would have to cancel and get simpler.
  This reasoning here contains several examples of number sense. It's all about being familiar with the patterns of numbers so you can apply them creatively in ways that will simply a problem. You may find this blog helpful.
  https://magoosh.com/gmat/2013/how-to-do-gmat-math-faster/
  Does all this make sense?
  Mike 🙂
  
  Reply
Mayank

January 20, 2015

this is the best possible explanation I have seen for this otherwise confusing and difficult topic. A gem indeed for related DS questions, thanks again !!!

Reply
1. Mike
  
  January 20, 2015
  
  Dear Mayank,
  You are quite welcome, my friend! 🙂 Best of luck to you in the future!
  Mike 🙂
  
  Reply
Tina

November 7, 2014

I’ve been confused about this since so long. Thanks this helped

Reply
1. Mike
  
  November 8, 2014
  
  Dear Tina,
  You are quite welcome! 🙂 I am very glad that we cleared up your confusion! Best of luck to you in the rest of your test prep!
  Mike 🙂
  
  Reply
Laura

October 16, 2013

Hi,
Isn’t the opposite? Since the fraction we are considering is x/y, x20, we are going to have a denominator much BIGGER than the numerator?

“We know y > 20 and x < 5. Well no matter what values we choose, we are going to have a denominator much smaller than the numerator. The larger possible fraction we could have under these constraints would be 4/21 (largest possible numerator with smallest possible denominator).'

Thank you,
Laura

Reply
1. Mike
  
  October 17, 2013
  
  Laura,
  Yes, the numerator would be much smaller than the denominator, the denominator would be much bigger, which means the fraction overall would have to be small. What I said was —of those small possible values for the fraction, the largest among them is 4/21. The fraction equals 4/21 or smaller. By giving a *largest* possible value, I am indicating how *small* the fraction is, not how large the fraction is. Does this make sense?
  Mike 🙂
  
  Reply
Adeel Yasin

August 25, 2013

Hi Mike,

Excellent work!

However, I feel that there is a typo in the paragraph Adding and Subtracting. Here is the original content,

Subtract a positive number from the numerator and/or add a positive number to the denominator of any positive fraction, and the new fraction will be greater than the starting fraction.

Here is what it should be,

Subtract a positive number from the numerator and/or add a positive number to the denominator of any positive fraction, and the new fraction will be SMALLER than the starting fraction.

Although, it is clear in the examples, but I think this typo may confuse others. Do you agree?

Reply
1. Mike
  
  August 25, 2013
  
  Dear Adeel,
  You are 100% correct. I just fixed that typo. Thanks for pointing it out!
  Mike 🙂
  
  Reply
John

May 14, 2013

I am confused. Lets see

4/6
decreasing nominator makes it smaller = 3/6
decreasing denominator makes it bigger = 4/5

but why decreasing both denominator and nominator at the same time makes it smaller?

Reply
1. Mike
  
  May 14, 2013
  
  John,
  The fraction 4/6 = 2/3 is less than one. If we *add* the same number to both the numerator & denominator, that moves it closer to 1, to the right on the number line, which makes it bigger. Thus, if we *subtract* the same number from both the numerator & denominator, that moves it further from 1, to the left on the number line, which makes it smaller.
  Another way to say it — start with 3/5 — add one to both the numerator & denominator, and it becomes 4/6 —- 4/6 is closer to 1 than 3/5, so it is bigger than 3/5, which means 3/5 is smaller than 4/6.
  Does all this make sense?
  Mike 🙂
  
  Reply
Faruk

August 6, 2012

Excellent article Mike…Very helpful indeed…:)

Reply
1. Mike
  
  August 7, 2012
  
  Thank you for your kind words, sir. Best of luck to you!
  Mike 🙂
  
  Reply
  1. Abhishek
    
    September 11, 2015
    
    Hi Mike,
    
    In the fraction properties module, I picked a rule i.e. when the same numerator is divided by a bigger denominator, this makes the overall fraction smaller. This seems correct. However, what if we have something like this
    case 1) numerator= 1, denominator = -2 so we have -1/2.
    case 2) numerator = 1 , denominator = 3 so we have 1/3.
    Now we notice that denominator 3 > -2 , yet the fraction remains greater 1/3 > -1/2.
    So the property relationship from increasing denominator may or may not lead to decrease in fraction. Am I tracking correctly?
    
    Reply
    1. Mike McGarry
      
      September 14, 2015
      
      Dear Abhishek:
      I’m happy to respond. 🙂 One stipulation about that rule that you seem to have overlooked: the rule only applies to positive fractions. With two positive fractions with the same numerator, the one with the larger denominator is smaller. If you have to figure out anything about two negative fractions, the easiest way is usually to compare the two absolute values, figure out that relationship, and then make everything negative again.
      If we are comparing any positive number to any negative number, it is absolutely pointless to use any rule other than the fact that (any positive) > (any negative). Using any fraction rules for this sort of comparison is a meaningless waste of time.
      Does all this make sense?
      Mike 🙂
      
      Reply