offers hundreds of GMAT video lessons and practice questions. Go there now.
Sign up or log in to Magoosh GMAT.

GMAT Permutations and Combinations

By on January 11, 2012 in Formulas, Permutations and Combinations, Quantitative

Permutations

A permutation is a possible order in which to put a set of objects.  Suppose I had a shelf of 5 different books, and I wanted to know: in how many different orders can I put these 5 books?  Another way to say that is: 5 books have how many different permutations?

In order to answer this question, we need an odd math symbol: the factorial.  It’s written as an exclamation sign, and it means: the product of that number and all the positive integers below it, down to 1.  For example, 4! (read “four factorial“) is

4! = (4)(3)(2)(1) = 24

 

Here’s the permutation formula:

# of permutations of n objects = n!

So, five books 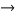right the number of permutations is 5! = (5)(4)(3)(2)(1) = 120

 

Combinations

A combination is a selection from a larger set.  Suppose there is a class of 20, and we are going to pick a team of three people at random, and we want to know: how many different possible three-person teams could we pick?  Another way to say that is: how many different combinations of 3 can be taken from a set of 20?

This formula is scary looking, but really not bad at all.  If n is the size of the larger collection, and r is the number of elements that will be selected, then the number of combinations is given by

# of combinations = 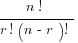{n!}/{r!(n-r)!}

 

Again, this looks complicated, but it gets simple very fast.  In the question just posed, n = 20, r = 3, and n – r = 17.  Therefore,

# of combinations = 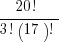{20!}/{3!(17)!}

 

To simplify this, consider that:

20! = (20)(19)(18)(17)(the product of all the numbers less than 17)

 

Or, in other words,

20! = (20)(19)(18)(17!)

 

That neat little trick allow us to enormously simplify the combinations formula:

# of combinations = 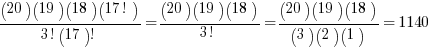 {(20)(19)(18)(17!)}/{3!(17)!}={(20)(19)(18)}/{3!}={(20)(19)(18)}/{(3)(2)(1)}=1140

That example is most likely harder than anything you’ll see on the GMAT math, but you may be asked to find combinations with smaller numbers.

 

Practice Questions

1) A bookseller has two display windows.  She plans to display 4 new fiction books in the left window, and 3 new non-fiction books in the right window.  Assuming she can put the four fiction books in any order, and separately, the three non-fiction books in any order, how many total configurations will there be for the two display windows?

  1. 24
  2. 72
  3. 144
  4. 336
  5. 420

 

2) The county-mandated guidelines at a certain community college specify that for the introductory English class, the professor may choose one of three specified novels, and choose two from a list of 5 specified plays.  Thus, the reading list for this introductory class is guaranteed to have one novel and two plays.  How many different reading lists could a professor create within these parameters?

  1. 15
  2. 30
  3. 90
  4. 150
  5. 360

Answers and Explanations

1) The left window will have permutations of the 4 fiction books, so the number of possibilities for that window is

permutations = 4! = (4)(3)(2)(1) = 24

 

The right window will have permutations of the 3 non-fiction books, so the number of possibilities for that window is

permutations = 3! = (3)(2)(1) = 6

 

Any of the 24 displays of the left window could be combined with any of the 6 displays of the right window, so the total number of configurations is 24*6 = 144

Answer: C.

 

2) There are three possibilities for the novel.   With the plays, we are taken a combination of 3 from a set of 5 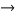right  n = 5, r = 2, n – r = 3

# of combinations = 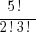{5!}/{2!3!} = {(5)(4)(3)(2)(1)}/{(2)(1)(3)(2)(1)} = {(5)(4)}/2 = 10

 

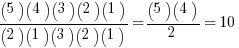
If the plays are P, Q, R, S, and T, then the 10 sets of two are PQ, PR, PS, PT, QR, QS, QT, RS, RT, & ST.

Any of the three novels can be grouped with any of the 10 possible pairs of plays, for a total of 30 possible reading lists.

Answer: B.

About the Author

Mike McGarry is a Content Developer for Magoosh with over 20 years of teaching experience and a BS in Physics and an MA in Religion, both from Harvard. He enjoys hitting foosballs into orbit, and despite having no obvious cranial deficiency, he insists on rooting for the NY Mets.

6 Responses to GMAT Permutations and Combinations

  1. Naren May 6, 2013 at 7:16 pm #

    Hi Mike

    Can we do it this way?

    1/3 * 2/5 * 1/4 = 1/30

    so we have 30 combination?

    Thanks

    Reply
    • Mike May 7, 2013 at 9:47 am #

      Naren,
      I assume you mean practice question #2. Yes, that would be another way to compute the number of possible reading lists.
      Mike

      Reply
  2. Rahul Sehgal March 24, 2013 at 11:00 am #

    Mike – Thanks for the valuable information. I have a clarification to make with respect to question 1.

    I was thinking – would not the answer be 24 + 6 = 30. I am thiking as she wants the ‘ficiton’ books still too be placed on the left hand side in any order and the same goes for ‘non fiction books.

    Am i missing a trick here ?

    Rahul Sehgal
    GMAT aspirant !!

    Reply
  3. Gopal September 10, 2012 at 1:40 pm #

    A nice intro to P&C and, probably you are true WRT the GMAT, this is probably more than enough to crack

    Reply
    • Mike September 10, 2012 at 5:21 pm #

      Thank you very much.
      Mike :-)

      Reply


Magoosh blog comment policy: To create the best experience for our readers, we will approve and respond to comments that are relevant to the article, general enough to be helpful to other students, concise, and written with correct grammar and spelling! :) If your comment was not approved, it likely did not adhere to these guidelines. If you are a Premium Magoosh customer and would like more personalized service, you can send us any questions you have through the Help tab in the product and we will respond quickly. Thanks!

Leave a Reply