Learn how to simplify these seemingly devilishly complicated GMAT Quant problems!
First, consider these problems
3) Consider these three quantities
Rank these three quantities from least to greatest.
- (A) I, II, III
- (B) I, III, II
- (C) II, I, III
- (D) II, III, I
- (E) III, I, II
These are challenging problems, especially the third one! With a few simple insights about factorials, though, you will be able to manage all of these.
The factorial
First of all, a few basics. The factorial is a function we can perform on any positive integer. The expression 5! (read “five factorial”) means the product of all the positive integers from that number down to one. In this particular case: 5! = 5*4*3*2*1 = 120. Here are the first ten factorials, just to give you a sense:
1! = 1
2! = 2*1 = 2
3! = 3*2*1 = 6
4! = 4*3*2*1 = 24
5! = 5*4*3*2*1 = 120
6! = 6*5*4*3*2*1 = 720
7! = 7*6*5*4*3*2*1 = 5,040
8! = 8*7*6*5*4*3*2*1 = 40,320
9! = 9*8*7*6*5*4*3*2*1 = 362,880
10! = 10*9*8*7*6*5*4*3*2*1 = 3,628,800
It’s a good idea to have the first five memorized, simply because those come up frequently on the GMAT —the first five are pretty easy to figure out on your own anyway. Nobody expects you to have the last five here memorized. I give them here purely to give you a sense of how quickly the factorials grow. By the time we get to (10!), we are already over a million! Similarly, (13!) is more than a billion, and (15!) is more than a trillion. Holy schnikes!
Operations with factorials
Here are some big ideas to help you when you have to perform arithmetic operations with factorials.
Big Idea #1: every factorial is a factor of every higher factorial
The number 73! must be divisible by 72!, by 47!, by 12!, etc. The number 73! automatically has at least 72 known factors — all the factorials less than it!
Big Idea #2: you can “unpack” one factorial down to another.
Think about 8! —- we know:
8! = 8*7*6*5*4*3*2*1
Well, by the Associative Law, we can group factors in any groupings, so we could insert parenthesis wherever we like. In particular , if I include a selection of factors that goes all the way to the right, all the way to 1, that’s another factorial. Thus:
8! = 8*(7*6*5*4*3*2*1) = 8*(7!)
8! = 8*7*(6*5*4*3*2*1) = 8*7*(6!)
8! = 8*7*6*(5*4*3*2*1) = 8*7*6*(5!) etc.
I chose 8! because we can see all the factors, but clearly we could extend this idea to any factorial, no matter how large:
237! = 237*236*(235!)
That’s an “unpacking” of the first two factors of 237! (BTW, this term, “unpacking”, is my own creation: you will not see this term used anywhere else.)
Big Idea #3: when you divide two factorials, you “unpack” the larger one, and cancel it with the smaller one.
Example:
Big Idea #4: when you add/subtract two or more factorials, you unpack them all down to the lowest one, and factor out that common factor.
For more on “factoring out”, see the section “Distributing and factor out” in this post.
Examples:
(200!) – (199!) = 200*(199!) – (1)*(199!) = (200 – 1)*(199!) = 199*(199!)
(200!) + (199!) = 200*(199!) + (1)*(199!) = (200 + 1)*(199!) = 201*(199!)
Summary
Having read these rules, give those three practice problems another try before reading the solutions below. Here’s a fourth problem, with its own video explanation.
4) http://gmat.magoosh.com/questions/811
Practice problem solutions
1) We are going to use the “factoring out” trick in both the numerator and the denominator:
Now, “unpack” that top factorial, to cancel the smaller one in the denominator:
Answer = D
2) “Unpack” the factorials in the numerator, so that everything is expressed as a product involving (89!) Then factor out that common factor.
Answer = D
3) Let’s consider the three expressions separately.
For expression I, we merely have to “unpack” the (49!) factor in the numerator.
So, expression I has a value of 49.
The expression II is tricky:
That’s a whole lot of factors in the numerator! That numerator is fantastically big: it has forty factors from 49 to 10 that are all greater than or equal to 10, so that means it’s automatically bigger than 10^40 (a number bigger than 1 trillion cubed — OMG!) That’s divided by 7! = 5040, so whatever this is, it’s way bigger than 49.
The expression III is a little easier than II:
That’s also a very big number. Each of the seven factors in the numerator is greater than 10, and 10^7 is ten million, so that numerator is more than 10,000,000. That’s divided by 7! = 5040. This is clearly bigger than 49. Notice, though, this has the same denominator as II, but many fewer factors in the numerator. Therefore II is much bigger than III.
Thus, from least to greatest, the order is I, III, II. Answer = B
Just as a note, if you are familiar with the idea of combinations, you may recognize expression II as a combinations number:
That would be the number of unique sets of 7 we could select from a pool of 49 unique items. There is no way you would be expected to calculate that number without a serious calculator or computer.
That’s a reasonably big number – just over 85 million. That’s a little more than a quarter the current population of the USA. For comparison, expression II is a real whopper:
This is a larger number than all humans and all other living things (animals & plants & all the way down to single-cell critters), including those alive now as well as those who have ever been alive on Earth. This number is larger than all the money in the world in pennies. This is more than the number of individual atoms comprising planet Earth and everything on Earth. This number is much much larger than the number of stars & planets & pulsars & quasars & black holes & whatever other star-like things in all galaxies & clusters in the visible Universe. The phrase “inconceivably big” does not even begin to capture how big this number is!

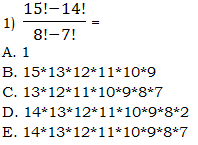

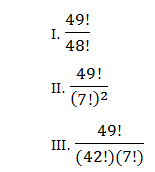

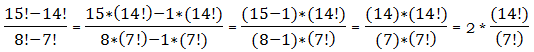
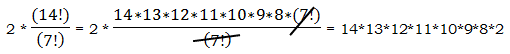
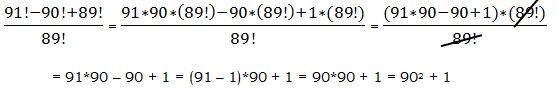

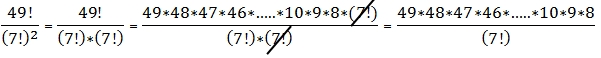
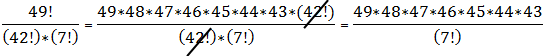

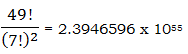




Leave a Reply